土力学新论：土体破坏极限面的外凸性及边界

岩土类材料在不同的应力作用下的强度各不相同，它们在图4.16所示应力空间的8个象限内的极限面也各不相同。如何用简单的数学公式来表达这个极限面是我们所要研究的复杂问题。极限面的外凸性为我们提供了研究的理论基础。Drucker公设（德鲁克公设或德鲁克定理）由美国科学院院士德鲁克（Drucker，1918—2001）于1951年提出[35]，现在已成为塑性力学的一个重要基础理论。由Drucker公设可得出屈服面必为外凸的曲面，屈服面的外凸性为强度理论的研究奠定了理论框架的基础。1967年，Palmer等[36]证明了Drucker公设可以推广到软化材料。20世纪80年代，中国科技大学李永池教授以及邓永琨教授等发表新的论证，也指出Drucker公设可以推广到软化材料并且可以应用于动力问题。

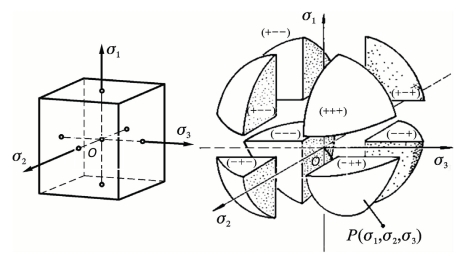
图4.16　应力空间的8个象限

根据Drucker公设，各种屈服准则的极限线必须是外凸的。屈服迹线可以是单一曲线，也可由各种不同的直线和曲线组成，并且能形成尖点。外凸性的示意图如图4.17所示。但是，屈服面的形状和大小并不是任意的，而需要根据实验结果和外凸性来确定，有一定的限制。

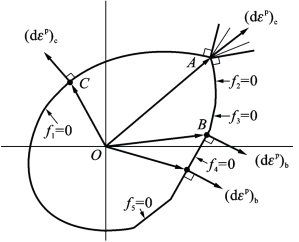
图4.17　Drucker公设的强度理论外凸性

根据Drucker公设，在应力空间中的屈服面必为外凸的曲面。如果在应力空间中的两个不同的应力矢量σij和存在下列条件：

式中，λ为一实数，满足条件0<λ<1，以坐标原点或坐标轴为参考，这一矢量σij的函数是外凸的。在一维情况下，不等式（4.1）的意义如图4.17及图4.18所示。

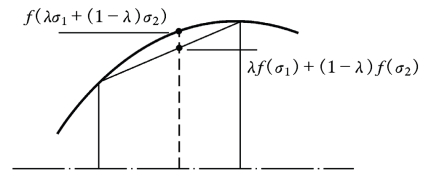
图4.18　屈服面的外凸性

可以看出，关于凸性的定义与人们日常对这个词的理解是一致的。但必须指明，凸和凹对于不同的参考系具有不同的含义。例如图4.19的凸函数，从下面的坐标轴往上看，它是外凸的，但从曲线上面往下看，它则是内凹的。为了一致，我们均以坐标原点或坐标轴作为参考系，如图4.19所示。

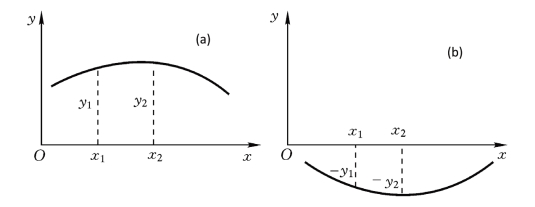
图4.19　外凸性与坐标；（a）y′′<0；（b）y′′>0

屈服面外凸性的更一般情况如图4.20和图4.21所示。以坐标原点为参考，图中屈服面处处外凸。屈服面上的任意应力点σij满足屈服条件f（σij）=0。若过任一应力点σij作屈服面切线A-A，则所有可能的、在屈服面内的应力点或屈服面上的应力点σij必在A-A面的一侧，此即为屈服面的外凸性。它也可以理解为在凸屈服面内任两点的连线仍在此曲面内。

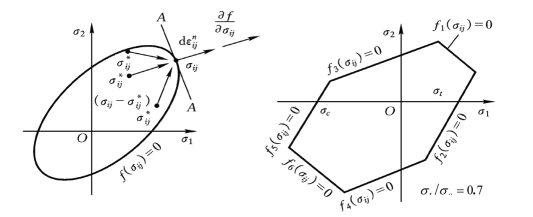
图4.20　外凸屈服面

根据Drucker公设，屈服面不可能是内凹的，如图4.21所示，但它可以由分段光滑的屈服函数共同组成一个屈服面，并且允许形成角点，如图4.22所示。此外，因为在屈服曲线之内应力变化是弹性的，因此，屈服曲线是单连通的。从坐标原点出发的应力状态矢不可能与屈服曲线两次相交。它也可以表述为：屈服面内任何两点的连线不会穿越过屈服面。反之，即为非凸形状，如图4.21的非凸屈服面所示。

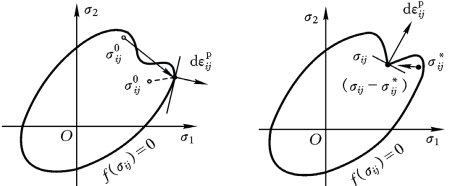
图4.21　非凸屈服面

图4.22　分段外凸屈服面

屈服面的外凸性也可由偏平面的屈服迹线来进行研究。对于岩土类材料，π平面上的极限曲线必须同时通过图4.23（a）中的a1、a2、a3、和a′3六个点。用不同曲线连接这六个点，就可以得到各种不同的多边形屈服线。不等边六边形必为最小范围的屈服线，而不可能是内凹的a1-n-a′3曲线。这一不等边六边形即为莫尔-库仑强度理论的极限面。强度理论的极限迹线的范围和内外两个边界在偏平面的表述如图4.23（b）所示。

此外，连接这6个点的屈服线的外凸线也应该具有一定的限度，因为在图4.23（a）中，如果连接a1和点的外凸曲线为屈服线，则根据屈服曲面的对称性，这时在a1点形成了内凹的尖点，这违反了屈服面的外凸性。

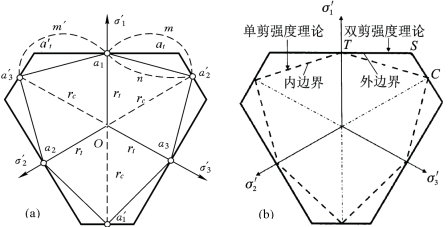
图4.23　屈服面外凸性（a）和内外边界（b）(www.xing528.com)

各种强度理论的极限迹线必须通过拉伸实验点σt和压缩实验点σc，并在内外两个不等边六角形之间，如图4.24所示。其中4.24（a）为1958年莫斯科大学Lvlev提出的拉压强度相同材料的极限面的范围，4.24（b）为1975年美国陆军弹道研究实验室Candland提出的拉压强度不同材料的极限面。

连接实验点（图4.24的五角星）的直线所组成的六边形内边界在理论上就是Tresca屈服准则和莫尔-库仑准则，它们分别为拉压强度相同材料（σt=σc）和拉压强度不相同材料（σt≠σc）屈服准则的下限，没有任何其他外凸屈服面可以小于它们。它们也可称为单剪理论，因为在数学模型方程中只有单一的剪应力被考虑。单剪理论表达式如下：

图4.24　外凸屈服面的内边界和外边界（平面应力表示）。（a）拉压强度相同材料（σt=σc）；（b）拉压强度不同材料（σt≠σc）

现在大家也知道，连接各实验点（图4.24的五角星）之间的两段直线所组成的六边形外边界在理论上就是双剪屈服准则和双剪强度理论，它们分别为拉压强度相同材料（σt=σc）和拉压强度不相同材料（σt≠σc）的屈服准则的上限。没有任何其他外凸准则可以大于双剪理论。

双剪屈服准则的数学表达式为：

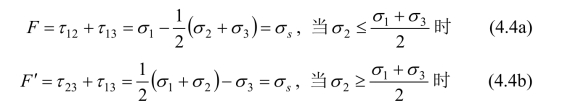
双剪强度理论的数学建模方程为：

双剪强度理论的主应力表达式为：

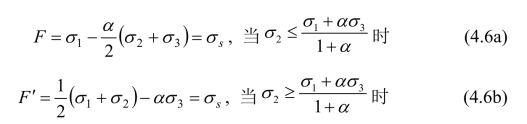
屈服面范围的确定具有重要的意义。由于历史原因，一般只了解岩土材料屈服面的内边界，如果在教学和研究中也了解岩土材料屈服面的外边界，那么在理论上就更加完善，也可以更好地理解实验结果[36-39]。几种可能的外凸屈服面如图4.25所示。

图4.25　几种可能的外凸屈服面。（a）线性极限迹线；（b）非线性极限迹线（曲线3和4）

应该指出，一般的曲线准则的范围达不到外边界，大多在内外边界区域的1/2到2/3范围内，超出这个范围就成为内凹的屈服面。因此，这些曲线准则事实上扩展不了全部范围，如称之为统一屈服准则，一般认为是一种局部统一屈服准则或“假”统一屈服准则。

由Drucker公设推论可知，外凸屈服面的外边界由两段直线组成。因此，外边界不能由一般曲线来表述，而需要用分段线性准则表述。例如，图4.26为两种三剪曲线形屈服面，它们的外凸屈服面只能扩展到比较小的范围，在很大区域内将成为非凸的屈服面，这与屈服面的外凸性相矛盾。因此，各种曲线统一准则不可能覆盖到全部外凸区域。

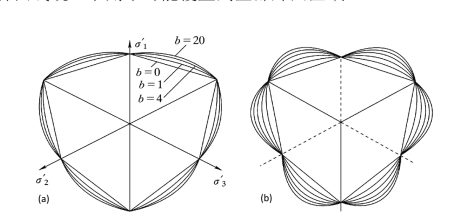
图4.26　两种三剪扩展准则。（a）三剪扩展准则只能覆盖部分区域；（b）三剪扩展准则的非凸屈服面

很多国内外学者对岩土材料在复杂应力的极限面都进行过大量的研究。实验得出的极限面一般都不符合莫尔-库仑强度理论，而是在莫尔-库仑强度理论和双剪应力强度理论的内外边界之间。部分实验结果将在下一章讨论。

以上这些基本特性中，有一些是相关的，如正应力效应中蕴涵了静水应力效应，双剪应力效应中蕴涵了中间主应力效应，中间主剪应力效应中蕴涵了中间主应力效应，双剪应力正应力效应中蕴涵了中间主应力效应和静水应力效应等。研究岩土材料在复杂应力作用下的这些基本特性，不仅对研究屈服准则和提出新的屈服准则有意义，而且对判断、选择和应用合理的屈服准则以及进行岩土结构分析也有重要的意义。

此外，应该指出，圆形极限线符合外凸性的要求，但是不能与三条拉伸极限线和三条压缩极限线同时匹配，因而与实验结果不符合，如图4.27所示。

图4.27　圆形极限线与两种岩石实验结果的比较