应力角效应：《土力学新论》中的重要成果

有意思的是，应力角效应的研究与中间主应力效应的研究相同，也是由现有的强度理论引起的。我们知道，对于各向同性材料，三个主应力变量（σ1，σ2，σ3）可以转换为三个应力不变量（I1，J2，J3），其中I1为应力张量第一不变量，J2为应力偏量第二不变量，J3为应力偏量第三不变量，应力角则与J3有关。因此，强度理论也应该与这三个作用量有关，可以写为这三个作用量的函数F=F（I1，J2，J3）。但是在1904—1913年出现的Huber-von Mises准则可以写为f=J2=C，而1952年提出的Drucker-Prager准则可以写为F=J2+βI1=C，它们分别只考虑了三个应力不变量（I1，J2，J3）中的一个或者两个，都没有将应力偏量第三不变量J3考虑进去。

这个问题比Tresca屈服准则和莫尔-库仑强度理论中的中间主应力效应问题更为复杂和难以发现，因为它们的主应力表达式中都反映了三个主应力（σ1，σ2，σ3），并且这两个准则的提出者都是世界著名的力学家。所以直到20世纪80年代，著名科学家Chen WF（陈惠发）和Zienkiewicz再次提出这个问题后，仍然没有得到足够的重视[23-27]。Chen和Zienkiewicz指出，岩土材料强度理论在偏平面的极限迹线不应该是一个圆（即圆形迹线与应力角无关），而是与应力角有关。俞茂宏分别于1992年和1998年详细分析了四种锥体的屈服面，即伸长锥、折衷锥、压缩锥和内切锥，并且指出它们与岩土材料之间的差别[28-29]。其中，图4.12为四种锥体与莫尔-库伦强度理论的屈服面的对比，图4.13为四种锥体与双剪强度理论的屈服面的对比，从图中可以清楚地看出这几种准则在偏平面和极限面的形状不同。

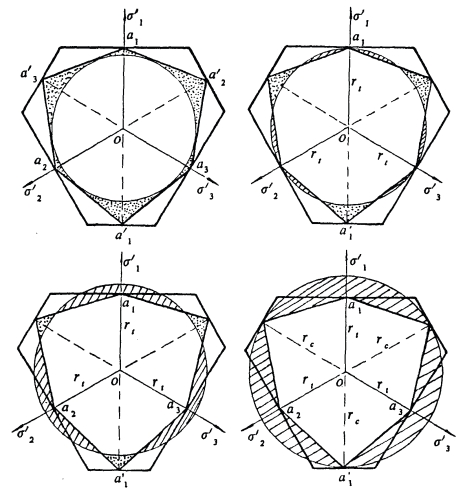
图4.12　四种锥体与Mohr-Coulomb强度理论的屈服面的对比

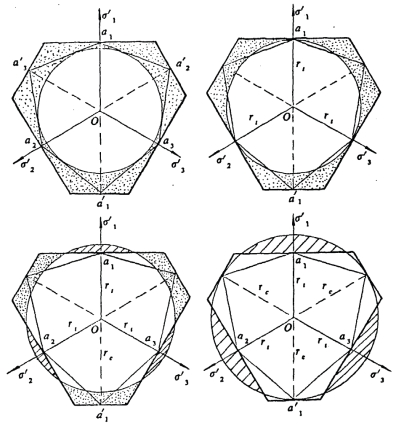
图4.13　四种锥体与双剪强度理论的屈服面的对比

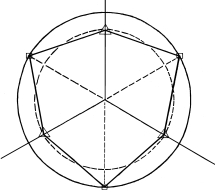
圆形屈服迹线都是外凸的。但是，圆形的迹线不能与岩土材料（σt≠σc）的三个拉伸实验点（三角形）以及三个压缩实验点（方状点）同时匹配，如图4.14所示。美国工程院院士Chen WF等指出，Drucker-Prager准则的优点是简单和光滑，但Drucker-Prager准则的圆形极限面与实验结果相矛盾。大量岩土材料的实验结果表明，岩土材料具有应力角效应（应力偏张量第三不变量效应），即它们的极限面与偏平面的交线不是圆形。从这一点来讲，Drucker-Prager准则不能满足应力角效应的条件。

(www.xing528.com)

图4.14　圆形的迹线不能与岩土材料的三个拉伸实验点和三个压缩实验点同时匹配

2002年，Davis和Selvadurai[30]指出 “如果在平面应力状态下，Drucker-Prager准则的差别会更大”，如图4.15所示。Drucker-Prager准则不能同时与两个拉伸试验点和两个压缩试验点相符合。2005年，Ottersen和Ristinmaa[31]指出：“应用Drucker-Prager准则应该小心谨慎。实际上，Drucker-Prager准则只能应用于拉压强度相差较小的材料。”拉压强度相差较小的材料实际上也就是接近拉压强度相同的材料，即σt=σc的材料，这时Drucker-Prager准则也就转换为Huber-Mises准则。2008年，Neto等[32]指出：“Drucker-Prager准则的外接锥和内切锥都不能很好地描述材料某些应力状态下的行为，其他近似准则可能更加适合。”2010年，英国皇家工程院院士Yu[33]指出；“Drucker-Prager准则在岩土工程分析中得到广泛应用，但是实验结果表明Drucker-Prager准则在偏平面的圆形迹线与实验结果不符合。因此，在岩土工程分析中应用Drucker-Prager准则需要十分谨慎。”2018年，俞茂宏[34]也特别指出：“偏平面为圆形的准则并不适用于岩土材料。”

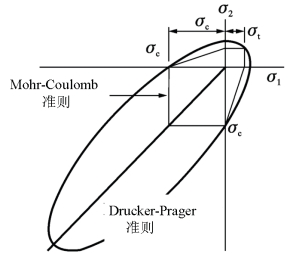
图4.15　Drucker-Prager准则不能与全部实验点匹配

Drucker-Prager准则是曲线型准则，因此在土力学问题的解析解和土力学教科书中并没有得到应用。近年来，国内外学者也提出了一些将本构模型加圆形作为破坏准则的外边界的理论，它们在理论上同样是不完整的。但是，由于Drucker-Prager准则被写入很多结构分析商用软件，应用十分方便，因此在计算力学和土力学的数值计算中得到了广泛应用。经过多年的实践，Drucker-Prager准则的问题已被逐步认识。英国皇家学会会员、皇家工程院院士、美国工程院院士和中国科学院院士Owen等在他们2008年的学术著作中特别指出[32]：“Drucker-Prager准则的外接锥和内切锥都不能很好地描述材料在某些应力状态下的行为。因此，根据要分析的特定问题中的主应力状态，其他近似准则可能更加适合。”他们还作出了与图4.13相似的图形来说明此问题。综上所述，现在可以认为，不考虑应力角效应的破坏准则在理论和实际上都存在着一定问题，需要十分谨慎，最好是不用。2018年，俞茂宏对这些问题进行了理论上的总结，提出了五点基本原则，并将其与一些典型破坏准则列表进行了对比[34]。

通过以上分析，我们还可以作出一个重要的结论：“圆形准则不可能成为岩土材料破坏准则的外边界，也不可能成为岩土材料破坏准则的内边界。”否则，那不仅在理论上是错误的，而且在具体应用上将会造成极大的错误。这些在本节众多著名学者Zienkiewicz、Chen WF、余海岁以及多国院士、著名计算力学专家Owen等都已发出警告，并将其写入他们的学术著作中。

这方面的一个工程实例是三峡水电站的高边坡船闸，科研人员曾经采用过各种破坏准则进行计算对比，最后决定采用Drucker-Prager准则作为设计准则，但结果是船闸隔离墩的底部几乎全部是计算“塑性区”，为解决此问题不得不采用大量的锚杆加固，将原本强度很高的岩石钻了很多的孔洞，穿过锚杆来浇筑高强度水泥浆。这样处理不仅增大了投资，延长了工期，而且其效果有待长期观察考虑。