岩土材料强度理论的一些研究主题往往由已有强度理论中存在的问题而引发。土体强度的中间主应力效应本来是一个不成问题的问题，因为土体在三向空间应力（σ1，σ2，σ3）作用下的强度自然与这三个作用量有关系，但是，最早出现的最大剪应力屈服准则（Tresca屈服准则，1864）的表达式f=σ1−σ3=σs及莫尔-库仑强度理论的表达式F=σ1−ασ3=σt都没有中间主应力σ2，当时也没有其他的理论，因此它们被广泛接受和了解，并在工程中被广泛应用。尽管这个问题在一开始就已经被提出，但中间主应力研究是一个十分困难的问题，因为中间主应力效应的应力试验研究设备更复杂，对试验技术的要求更高，研究的经费投入更多。此外，中间主应力效应往往综合反映在静水应力效应等实验中，若要把它独立出来，就需要有明确的概念，而在理论上要提出一个有一定的物理概念、数学表达式简单且反映中间主应力效应的新的强度理论并非易事。
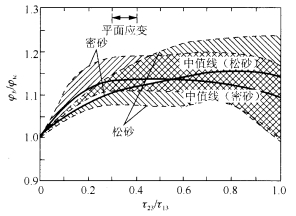
实验得出的π平面的极限线均大于莫尔-库仑强度理论的极限线。同济大学、河海大学、西安理工大学等研制了土的真三轴仪，并进行了上海黏性土、黄土等的真三轴试验研究。在土的中间主应力效应方面，现在大量的实验结果已经证实该效应的存在。日本京都大学的Shibata和Karube于1965年发表了黏土的研究结果，认为黏土的应力应变曲线的形状与σ2有关。英国剑桥大学、帝国理工学院以及Glasgow大学等得出的一系列试验结果也与莫尔-库仑强度理论不相符合。图4.10是李广信总结的砂的中间主应力效应[22]。中间主应力效应可以派生出中间主剪应力效应。中间主剪应力效应以前较少被研究，近年来已经有了一些研究报道，它的规律与中间主应力效应相同。
图4.11为Kwasniewski和李小春等对砂岩的中间主剪应力效应的研究结果[22]，两图中的横坐标分别为τ23/τ13和τ23=（σ2−σ3）/2（也可取τ12=（σ1−σ2）/2），纵坐标分别为材料的内摩擦角和剪切强度τ13=（σ1−σ3）/2。其他学者的实验结果也可以转化得出关于土的中间主剪应力效应的研究结果。
(www.xing528.com)
图4.10 砂的中间主应力效应（李广信 2005）
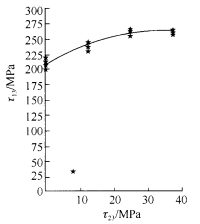
图4.11 砂岩的中间主应力效应（Kwasniewski等）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
