土力学新论-均布条形荷载技术提升

在实际工程中经常遇到的是如图3.11（b）所示的条形荷载。均布条形荷载p0沿x轴上某微分段dx上的荷载可以用线荷载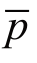代替，并引入OM线与z轴线的夹角β，得：

则地基中任一点M处的附加应力用极坐标表示如下：

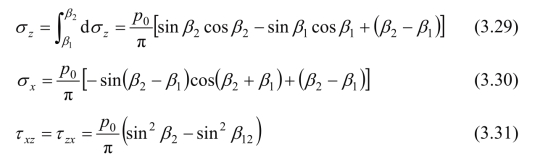
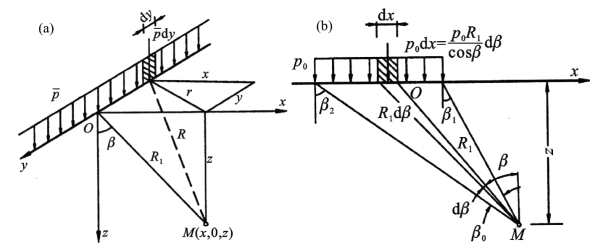
图3.11（a）线荷载作用；（b）均布条形荷载

当M点位于荷载分布宽度两端点之间时，β1取负值，反之则取正值。

将式（3.29）−（3.31）代入材料力学公式，可得M点的大、小主应力σ1和σ3的表达式：

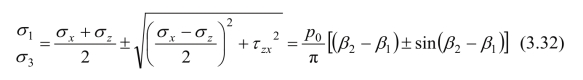
条形荷载引起附加应力的大、小主应力如图3.12所示，大、小主应力作用的方向分别与这个张角的角平分线方向平行和垂直。图中所示的各个应力椭圆的长短轴的方向和长短分别表示不同位置大、小主应力方向和大小。大、小主应力的等值线是过条形基础边缘两点的圆弧，圆弧上各点对此弧的圆周角相等。

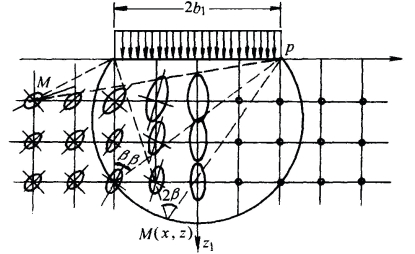
图3.12　条形荷载引起附加应力的大、小主应力方向和应力椭圆

为了计算方便，还可将公式（3.29）−（3.31）改用直角坐标表示。此时取条形荷载的中点作为原点，则三个应力分量如下：

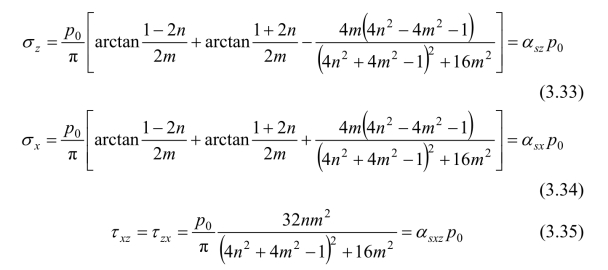
式中，αsx、αsz和αsxz分别为均布条形荷载下相应的三个附加应力系数，都是n=x/b和m=z/b的函数。(www.xing528.com)

利用以上有关各式可绘出σz、σx和τxz等值线图，这种椭圆球形状的曲线也称为应力泡，如图3.13所示。

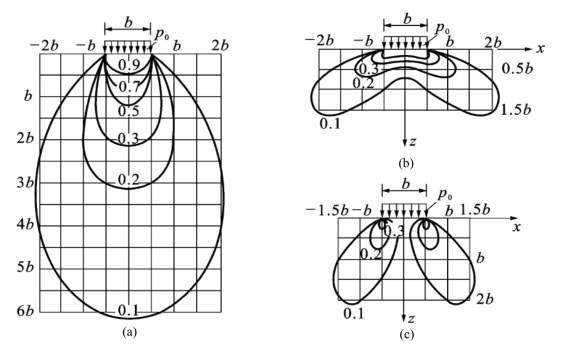
图3.13　均布长条形荷载下地基附加应力σz（a），σx（b）和τxz（c）等值线

为了对地基附加应力分布有更全面的了解，我们在下面给出了其他一些典型荷载下的各种不同地基附加应力图的σz等值线图（应力泡）。图3.14为集中荷载Q作用下的σz等值线图，图3.15为线荷载P作用下的σz等值线图。

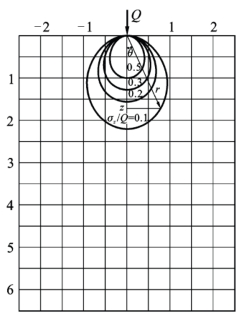
图3.14　集中荷载Q作用下的σz等值线图

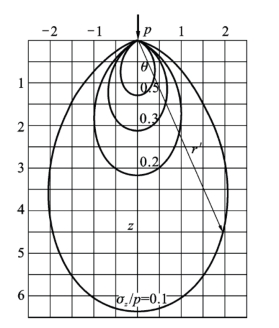
图3.15　线荷载P作用下的σz等值线图

图3.16为L=1.5B和L=2B的长方形均布荷载作用下的σz应力等值线图，图3.17为L=3B和的L=∞（L足够长时）均布荷载作用下的σz应力等值线图。根据这些图，可以判断出建筑物具有不同的长宽比时，地表面的荷载在地基中引起的附加应力的影响范围。由图3.16（b）可知，当L=2B时，垂直方向附加应力为−0.1p时的影响深度增加到3B左右。由图3.17（b）可知，条形荷载（L=∞）的垂直方向附加应力为−0.1p时的影响深度增加到6.3B左右。

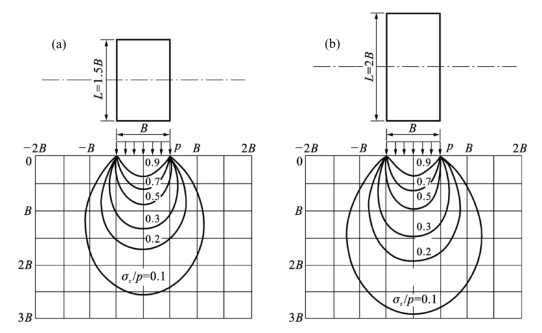
图3.16　长方形均布荷载作用下的σz等值线图。（a）L=1.5B；（b）L=2B

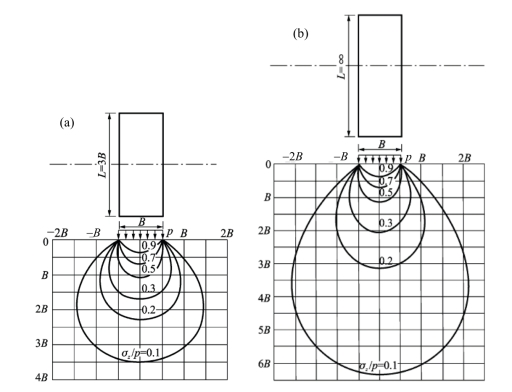
图3.17　长条形均布荷载作用下的σz等值线图。（a）L=3B；（b）L=∞