土力学新论：静水应力轴

由于材料的力学性能往往与静水应力的大小有一定的关系，因此在强度理论的研究中，特别是在岩石、土体、混凝土破坏准则和本构关系的研究中，常常采用以静水应力轴为主轴的应力空间，如图2.12（a）所示，图中主轴为静水应力轴或z轴；π平面的坐标则可取（x，y）为直角坐标，或（r　θ，）为极坐标，如图2.12（b）所示。

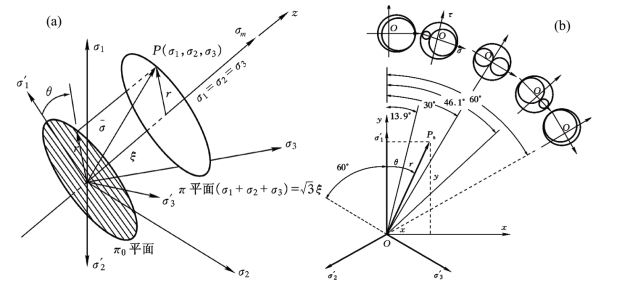
图2.12（a）柱坐标；（b）π平面上的应力状态

因此，主应力空间的应力点P（σ1，σ2，σ3）可表示为P（x，y，z）或P（ξ，θ，r），它们与主应力、主剪应力以及静水应力轴坐标之间的关系如下：

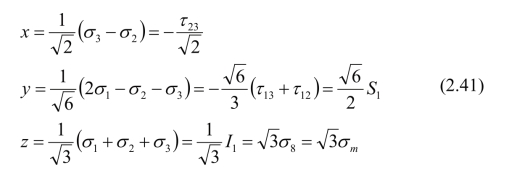
柱坐标（ξ，θ，r）各变量与主应力P（σ1，σ2，σ3）之间的关系为：

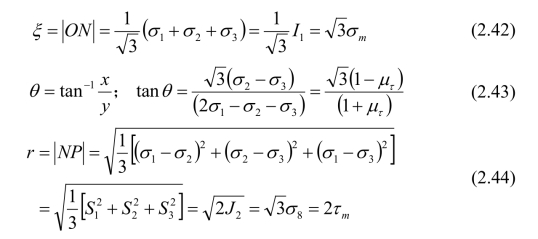
由式（2.41）和（2.43）可得出：

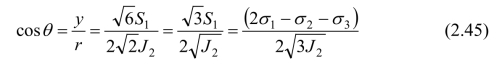
注意到应力偏量第二不变量J2和应力偏量第三不变量J3分别等于J2=-（S1S2+S2S3+S1S3）和J3=S1S2S2，由三角关系可得：

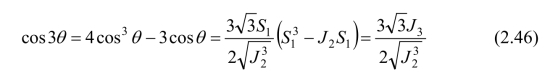
三个主偏应力可推导得出：

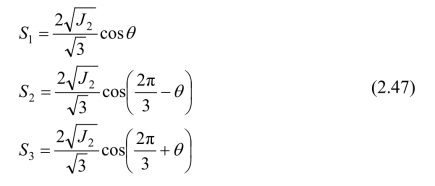(www.xing528.com)

以上关系只有在σ1≥σ2≥σ3和0≤θ≤π/3的条件下才适用。以后我们可以看到，对于各向同性材料，在π平面上的材料极限面具有三轴对称性，因此一般只要了解在60°范围内的材料特性或极限面，即可按三轴对称性作出整个π平面360°范围的材料极限面。

由式（2.42）、式（2.45）−（2.47）及偏应力概念得出相应的三个主应力为：

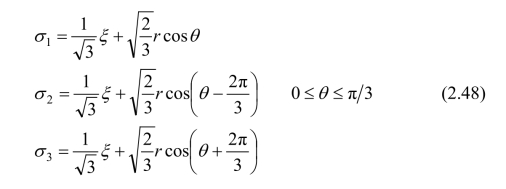
如用应力张量第一不变量I1和应力偏量第二不变量J2表示，式（2.48）亦可表示为：

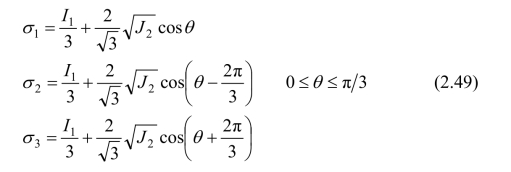
三个主剪应力亦可相应推导得出：

使用以上各式可以方便地研究π平面上各应力分量之间的关系，并且可以建立起三个主应力独立量（σ1，σ2，σ3）和三个应力不变量（J1，J2，J3）或应力空间柱坐标三个独立量（ξ，θ，r）之间的关系，以及它们与应力状态参数（双剪应力状态参数或Lode应力参数）之间的关系。表2.2总结了几种典型的应力状态特点和应力状态参数以及应力角θ的关系。

表2.2　应力角与应力状态参数的关系

图2.11（b）同时绘出了与不同应力角相对应的几种典型应力状态的三向应力圆。应力圆的纵坐标τ均对应于π平面的应力状态，即相对于静水应力σm=C/3的状态。因此，当加或减一个静水应力时，应力圆的相对大小和位置均不变。

由于材料的强度以及强度极限面往往随静水应力而变化，因此便于在柱坐标（ξ，θ，r）中研究极限面。