土力学新论：主应力空间与应力状态矢量的关系

单元体的主应力状态（σ1，σ2，σ3）可用σ1—σ2—σ3直角坐标中的应力点P（σ1，σ2，σ3）来确定，如图2.10所示。应力点的矢径OP为：

式中，ei为坐标轴的正向单位矢。

通过坐标原点作一等斜的π0平面，π0平面的方程为：

图2.10　应力空间和应力状态矢量

在π0平面上所有应力点的应力球张量（或静水应力σm）均等于零，只有应力偏张量。π0平面的法线ON称为等倾线，它与三个坐标轴成54°44′等倾角，其方程为：

应力张量σij可以分解为球张量和偏张量，应力状态矢σ也可分解为平均应力或静水应力矢量σm和平均剪应力矢量或均方根主应差τm，如式（2.34）和图2.11所示，以及它们的大小（模）分别为：

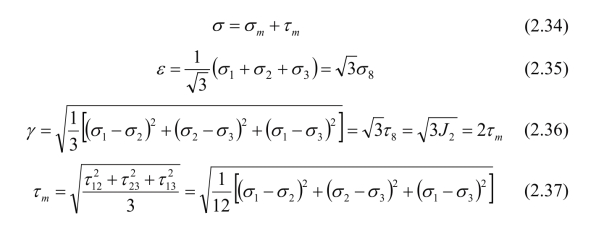(www.xing528.com)

平行于π0平面但不通过坐标原点的平面称为π平面，其方程式为：

式中，参数C为任意常数。π平面上各应力点都具有相同的应力球张量（或静水应力σm=C/3），且平行于静水应力线但不通过坐标原点的直线方程为：

式中，C1、C2和C3为三个任意常数，沿这条直线上的各点具有相同的应力偏量。因此，对于与静水应力σm无关的问题可以在π平面上进行研究。

图2.11　等倾偏平面

应力空间三个主应力坐标轴（σ1，σ2，σ3）在π平面上的投影为（σ′1，σ′2，σ′3），它们之间的投影关系可以通过应力在等斜面上的投影得到。在图2.11中，ABC为等斜面，ON为等倾线，且两者正交，OO′分别与直线O′A，O′B和O′C成直角。等倾线ON与三个应力坐标轴之间的夹角都相等，即为。因此，可得π平面上的（σ′1，σ′2，σ′3）坐标与应力空间的三个坐标轴（σ1，σ2，σ3）之间的关系如下：

剪应力τm恒作用在π平面上，它在（σ′1，σ′2，σ′3）轴上的三个分量存在关系：S1+S2+S3=0，因此它只有两个独立分量。只要知道τm的模和它与某轴的夹角，或它在π平面上一对垂直坐标（x，y）的两个分量，即可确定τm。