在土力学和土工试验中,一般采用常规三轴试验(轴对称三轴试验)得出土体材料的强度指标摩擦角φ。但是,Wade以及Cornforth[17]进行砂土的平面应变试验时发现,砂土在平面应变条件下得出的土体材料的强度指标φ平面应变比常规三轴试验得出的土体材料强度指标φ三轴大很多。1966年,Henkel和Wade[18]进行了饱和重塑黏土的平面应变试验,又得出同样的结果。1974年,Al Hussaini[19]进行了砂的平面应变试验;1977年,Vaid和Campanella[20]进行自然黏土的平面应变试验,他们也都得出了同样的结果。图1.20(a)为Cornforth[17]进行的不同孔隙率砂土的平面应变试验(试件在σ1>σ2>σ3应力状态下的剪切破坏)和常规三轴试验(试件在σ1>σ2=σ3应力状态下的剪切破坏)得出的结果。Al Hussaini[19]对不同密度砂土进行了平面应变试验和常规三轴试验的对比,结果如图1.20(b)所示。Cornforth和Al Hussaini的试验结果得出的强度指标摩擦角φ也都有明显的差别,这些都是由于中间主应力不同引起的。
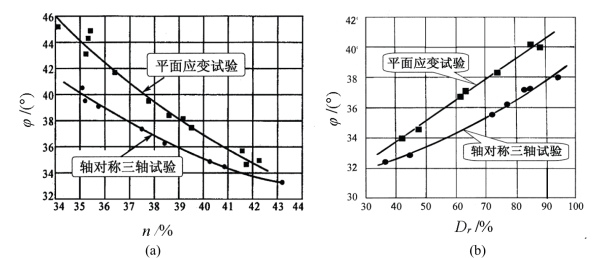
图1.20 两种试验的摩擦角变化。(a)Cornforth(1964);(b)Al Hussaini(1973)
平面应变试验和常规三轴试验两种试验结果得出的抗剪强度指标有明显的差别。这种现象很快被中国土力学之父、清华大学黄文熙先生注意到,他研制了平面应变试验机,并指导研究生李树勤等进行了“在平面应变条件下砂土本构关系的试验研究”,得出了明确的结论[21]:“无黏性土在平面应变条件下的本构特性与轴对称条件下有较大差别。在研究土的本构关系时不能忽视这些差别。”
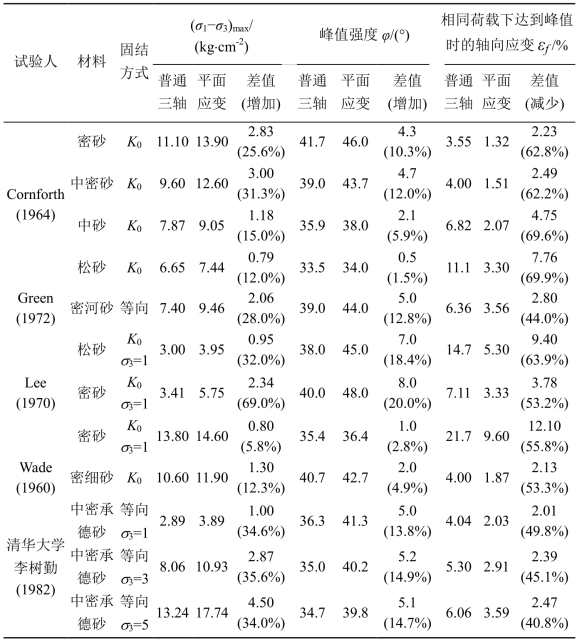
表1.2给出了国内外最早进行的关于砂土的平面应变试验相对于轴对称三轴压缩的强度和变形的变化结果。可以看到,砂的平面应变试验得出的峰值强度(摩擦角φp)一般比轴对称三轴强度摩擦角φ大1.0°~7.0°,提高了2.8%~18.4%;而相同荷载下峰值的轴向应变ε则减少2.47~9.4(以轴对称三轴压缩下的峰值为例),即降低了40.8%~63.9%。
表1.2 砂的平面应变试验相对于三轴压缩的强度和变形的变化(https://www.xing528.com)
清华大学、河海大学、同济大学和中国水利水电科学院等高校及科研院所的学者都进行了平面应变问题的研究。马险峰等基于大阪市立大学真三轴压缩试验装置开发了改良型平面应变仪,这种试验装置便于试样的放置,尤其是对于自立性较差的松散砂或软黏土试样可同时进行拉伸试验。他们进行了砂的平面应变与轴对称三轴围压试验,并总结出不同研究者的关于内摩擦角的结果,如图1.21(a)所示[22]。
国内外的研究者也都得出了一致的试验结果,如图1.21(b)所示[22],并且他们的分析结果也相同。他们都指出:平面应变试验与轴对称围压试验的差别,主要在于中间主应力的不同。中间主应力对土体本构关系是有影响的。在理论上,这种影响将通过破坏准则反映到土体的本构关系中。清华大学陈仲颐、周景星、王洪瑾,北京交通大学赵成刚、白冰和王远霞等以及李广信、张丙印和于玉贞的土力学将平面应变试验的主要结果写进土力学教科书中[23-24],并指出:“两种试验结果得出的抗剪强度指标φ有明显的差别。这种差别就是由中间主应力不同引起的。由于莫尔-库仑理论存在着这种缺点,所以人们不断地致力于更完善的强度理论的研究与探索。”
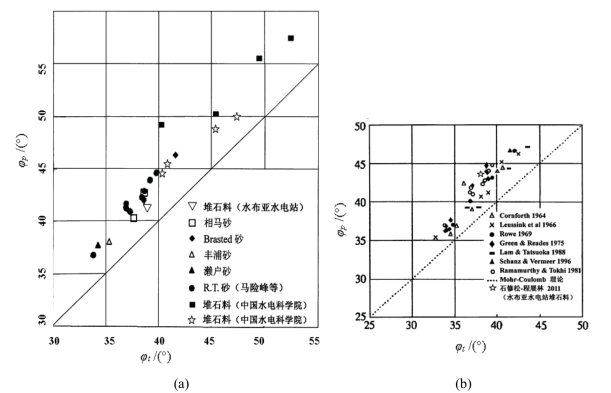
图1.21 常规三轴和平面应变实验下材料的内摩擦角。(a)砂土;(b)砂土和堆石料
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




