线性时不变系统状态方程解及其应用

如果系统矩阵A的元素为常量，即与时间无关，这样的系统称为时不变系统。现考虑一常系数（时不变）齐次状态方程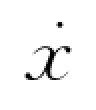：=Ax。

其解是：x（t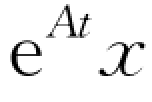）=（0），或者是：

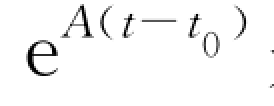是一个与矩阵A同阶的矩阵，且满足：

故e A（t-t 0）（或e At）是一个变换矩阵，它把初始状态矢量x（t 0）[或x（0）]变换为另一状态矢量x（t）。由于e A（t-t0）是一个时间函数矩阵，于是随着时间的推移，将不断地把初始状态矢量变换为一系列的状态矢量，从而在状态空间形成一条轨迹。从这个意义上讲，矩阵的指数函数e A（t-t 0）起着一种状态转移的作用，所以把它称为状态转移矩阵，并用符号φ（t-t 0）或φ（t）表示。

计φ（t-t 0）=e A（t-t0），状态转移矩阵的性质较多，一般有：

（1）φ（0）=e A·0=I。

（2）φ（t 2-t 1）φ（t 1-t 0）=φ（t 2-t 0）。

（3）φ（t-t 0）必有逆，且其逆为φ（t 0-t），即：φ-1（t-t 0）=φ（t 0-t）。

（4）φ（t 1+t 2）=φ（t 1）φ（t 2）=φ（t 2）φ（t 1）。

（5）[φ（t）]n=φ（nt）。

对于矩阵的指数函数的计算方法较多，分别有：

（1）按照e At的定义计算：e At=I+At+（A 2/2！）t 2+…，来计算e At的近似值。此法计算步骤简单，程序容易编制，适合于计算机计算，但在计算过程中要考虑收敛性的要求。此外，用此法不能获得精确的解析形式结果。

（2）按照拉氏逆变换计算：e At=L-1[（SI-A）-1]。此法虽能得到精确的封闭解，但有时矩阵A的阶数较高时，必须借助于计算机，而利用计算机计算（SI-A）-1 也并非是一件简单的事。(https://www.xing528.com)

（3）对角线矩阵和约当矩阵的矩阵指数函数的计算。

（4）化矩阵A的对角线标准形式或约当矩阵再计算e At。

（5）应用凯莱-哈密顿（Cayley Hamilton）定理化e At为A 的有限多项式。

即由凯莱-哈密顿（Cayley Hamilton）定量化e At为A 的有限多项式：

由于本文计算e At的方法就采用此法，所以下面分两种情况来介绍a j（t）（j=0，1，…，n-1）的计算方法。

情况1：A的特征值λ1，λ2，…，λn 互异。

可由下列等式：

求解得：

情况2：A的特征根有重根。

如果A的特征根λ1 为γ重根而其余n-r个是单根，对于重根部分有方程组：

式（3．45）连同其余n-r个单根方程可用来求解系数a j（t）（j=0，1，…，n-1）。