当火车疾驶经过车站时,车站上的人会觉得火车的汽笛声发生了变化:当火车奔向我们而来时,汽笛声便越来越尖;当火车离我们远去时,汽笛的音调又逐渐降低。1842年,奥地利物理学家多普勒(Christian Johann Doppler,1803~1853年)首先阐明造成这种现象的原因。他指出:当火车趋近我们时,每秒钟到达我们耳朵里的声波个数就比火车静止时多,因为这些声波除了从静止声源(汽笛)出发时按正常速度传播外,另外还附加了火车行驶的速度;而当火车离去时,每秒钟传到我们耳中的声波数目要比火车静止时少些,因为这些声波传来的速度变慢了,它等于声源(汽笛)静止时的声速减去列车的速度。总之,汽笛声的音调变化,乃是由于声源的运动使每秒钟撞击我们耳膜的声波数目发生了变化。这种现象,就称为“多普勒效应”。
多普勒效应不仅适用于声波,而且也适用于光波。一个高速运动的光源发出的光,到达我们的眼睛时,其波长和频率也发生了变化,也就是说它的颜色会有所改变。多普勒本人就曾指出:恒星的颜色必定会按它接近或远离我们的速度不同而发生不同程度的变化。这种看法原则上显然是无可非议的,可是实际上却不尽然。因为恒星运动的速度要比光速小得多,所以由恒星运动造成的光波波长变化是微乎其微的,它们根本不会导致恒星的颜色发生任何可察觉的变化。
1848年,法国物理学家斐佐(Armand Hippolyte Fizeau,1819~1896年)指出:观测光波的多普勒效应,最好的办法乃是测量光谱线位置的微小移动。当恒星趋近我们时,有如火车向我们驶来,这时星光的“光调”也会升高,也就是光波的频率增高,波长变短,于是光谱线往光谱中的紫端(波长较短的一端)移动;反之,当恒星远去时,光谱线便向光谱的红端移动,因为这时“光调”降低,频率低了,波长就变长(图58)。天文学家们通过测定光谱线“红移”或“紫移”的程度,便能计算出恒星在观测者的视线方向上趋近或离去的速度,这就是所谓的“视向速度”。
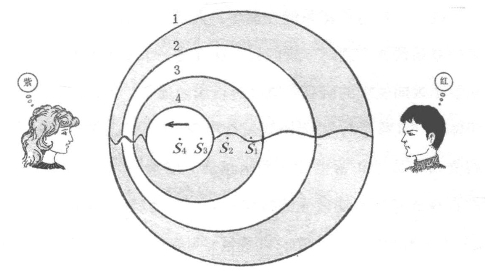
图58 光波的“多普勒效应”原理图
当光源朝向观测者运动时,观测者将发现光波的波长变短,于是光谱线往整个光谱的紫端移动;当光源远离观测者而去时,观测者将发现光波的波长变长,于是光谱线便向光谱的红端移动
1868年,英国天文学家哈金斯(William Huggins,1824~1910年)首先测得天狼星正以46.5千米/秒的速度远离我们而去。如今我们知道,天狼星其实是以8千米/秒的速度朝向我们而来,所以哈金斯测得并不准。然而,这毕竟是第一次尝试。因此,哈金斯的工作在天文学史上仍然占有光荣的一席。1890年,美国天文学家基勒(James Edward Keeler,1857~1900年)测出了大角星(牧夫α)正以6千米/秒的速度朝我们靠拢。这个数字说明当时的测量水平已经很高,如今我们知道大角星正以5千米/秒的视向速度向着我们而来。
利用多普勒效应也可以研究星系的运动。1912年,美国天文学家斯莱弗(Vesto Melvin Slipher,1875~1969年)发现,仙女星系M31正以约200千米/秒的速度向我们奔驰而来。可是两年以后,当他测出了15个星系的视向速度后,发现其中竟有13个星系都在以几百千米每秒的速度远离我们而去,在这些星系的光谱中,光谱线都有红移。然而,为什么这么多的星系都要“逃离”我们呢?这确是一个令人费解的问题。
对星系视向速度的研究在继续进行着。通常,人们用字母z来代表一个天体的“红移量”,或者干脆就简称为“红移”。它可以这样来计算:如果将光谱中处于正常位置(即未移动)的某一光谱线的波长记作λ0,由于存在视向速度而使该光谱线移动到波长为λ的位置上,则两者之差(λ-λ0)为波长位移的净大小,红移量z与它们有着如下的关系:
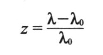
另一方面,红移z和视向速度υr成正比,写成公式就是:
![]()
其中c是光速,为300 000千米/秒。[1]
1929年,哈勃研究了业已用前述各种方法确定距离的24个星系的红移。结果发现距离越远的星系红移越大;而且,距离和红移之间有着良好的正比关系,这便是著名的“哈勃定律”。哈勃定律既可以用图的形式来表示(图59),也可以写成如下的简单公式:
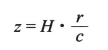
即(https://www.xing528.com)
![]()
或者
![]()
其中c是光速,r是星系的距离,z是星系的红移,υr是星系的视向速度。
H是一个比例常量,称为“哈勃常量”。哈勃常量要根据天文观测来推算,但它的具体数值很不容易定准。例如,1974~1976年,美国天文学家桑德奇(Allan Rex Sandage,1926~2010年)等人曾采用多种不同的方法,推算得出H=55千米/秒/百万秒差距。它的意思就是说,河外星系的距离每增加1百万秒差距,它退离我们的视向速度便增加55千米/秒。
2009年5月,美国国家航空航天局发布新得出的哈勃常量值H=74.2千米/秒/百万秒差距,其不确定度在5%以内。2013年3月,欧洲空间局又宣布最新推算得出的结果:H=67.80千米/秒/百万秒差距,误差值为±0.77千米/秒/百万秒差距。
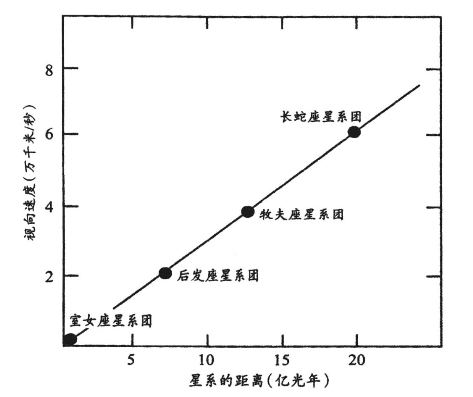
图59 哈勃定律
越远的星系退离我们的视向速度就越大,因而其红移也越大
有了哈勃定律,我们就可以通过观测河外星系的光谱,测量出它的光谱线的红移量,进而求获它的距离了。
容易明白,我们可以将一个星系团或星系群中任意一个成员星系的距离看作整个星系团或星系群的距离。这种情况,同前面介绍的把星团或星系中某一成员星的距离视为整个星团或星系的距离是很相似的。
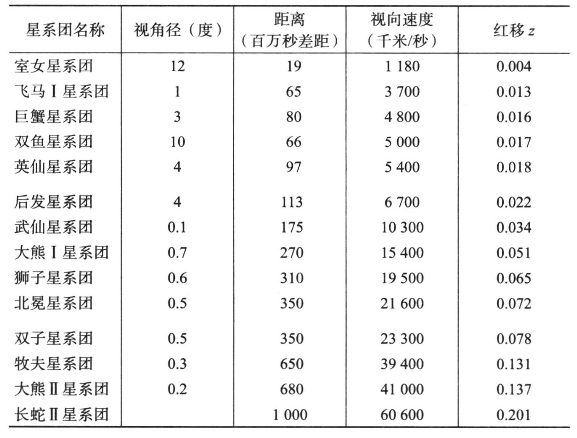
在前文的表5中,已经列出一些较亮星系(不包括本星系群中的星系)的名称、类型、视星等、大小、距离和视向速度。表8列出了一些星系团的概况。
表8 一些星系团的概况
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




