星星离我们有多远：集体贡献及星等差异

当星团或星系十分遥远时，我们无法分辨其中的单颗恒星，当然也无法用单星来确定它们的距离。这时，除了“从大小知远近”外，还可以利用星团和星系的“累积星等”求出距离。

累积星等代表了把星团或星系中的全部恒星统统加在一起究竟有多亮，这是一种“集体的贡献”。它也可以用视星等和绝对星等来表示。这时，尽管每颗星的光芒已暗不可见，但它们联合起来却仍使整个星团或星系耀然天际。

对于已经求出距离的每个球状星团，当然可以从它们的视星等一一求获绝对星等。结果发现球状星团的平均绝对星等约为-7.4等。如果认为距离尚未知晓的球状星团的平均绝对星等亦为-7.4等，那么又可以反过来，将它与视星等进行比较从而得出距离。利用这一方法，可测出数千万秒差距（上亿光年）远的球状星团及其所在星系的距离。

关于如何求球状星团距离的方法，我们就介绍到这里为止。表6选列了一些球状星团的视亮度、大小和距离。应该指出，在球状星团的中央，恒星很密集；越向外围，恒星分布的密集程度就越低；到接近星团边缘处，恒星的分布就非常稀疏了。也就是说，球状星团其实并没有一个很明锐的边界。因此，要确定一个球状星团的直径究竟有多大，实在是非常困难的。为了克服这种随意性，天文学家们想了一个办法，那就是用“有效半径”来表征球状星团的大小，有效半径的定义是：球状星团在此半径范围内的光亮度正好占星团的总亮度之半，因此它又称为“半光半径”。表6中的第3列给出的便是球状星团的“有效角半径”。

至于不同的星系，累积绝对星等的差异很大。哈勃曾按外形的不同将星系分为三大类，即旋涡星系、椭圆星系和不规则星系。旋涡星系具有旋涡状的结构，中心区域呈透镜状，周围绕有扁平的圆盘，从星系核心部分伸出若干条螺旋状“旋臂”，叠加到圆盘上（图57）。椭圆星系呈椭球形或圆球状，中心区域最亮，向边缘亮度逐渐减小。不同椭圆星系的质量差异非常大，质量最小的矮椭圆星系仅与球状星团相仿，大致相当于100万个太阳；质量最大的超巨椭圆星系则可达太阳质量的数万亿倍。不规则星系的外形不规则，也没有明显的核心和旋臂，在全天的亮星系中它们只占5%左右。仙女星系M31和银河系都是旋涡星系，大小麦云则均属不规则星系之列。

表6　一些球状星团的视亮度、有效半径和距离*

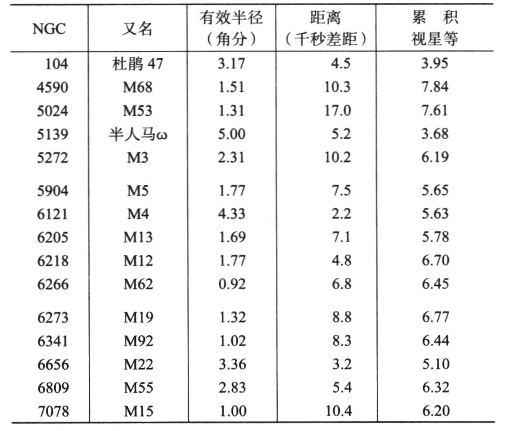
*表中NGC 104又名杜鹃47，NGC5139又名半人马ω，人们起初以为它们是单个的恒星。本表资料来源可参见http：//physwww.mcmaster.ca/～harris/mwgc.dat。

(www.xing528.com)

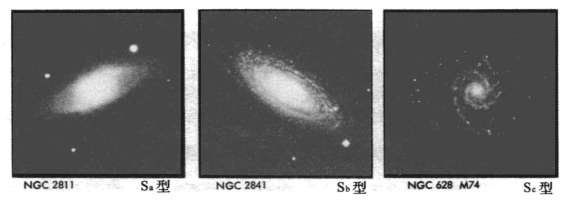
图57　旋涡星系可以分为三种次型，分别称为Sa型、Sb型和Sc型

Sa型（左图）的旋臂缠绕得最紧、Sb型（中图）的旋臂比较舒展，Sc型（右图）的旋臂最为松开

我们关心的，是各类星系的累积绝对星等，它们的情况如表7所示。可以认为待测距离的那个星系的绝对星等，就等于它所属那种类型的星系的平均绝对星等，于是与视星等相比较，距离问题便迎刃而解了。

表7　各类星系的累积星等

当然，因为各类星系绝对星等的范围都扩展得很广，所以这种方法仍然不是很准确的。不规则星系和旋涡星系的情况较好，按此测出的距离与实际情况至多不过相差三四倍；椭圆星系则有可能差到二三十倍。

读者已经看到，在走向离我们数亿光年甚至数十亿光年的极遥远星系时，人们是如何成功地攻克了一个又一个难关，我们的接力跑如何一棒又一棒地往下传。现在，我们依然在这条通往百亿光年之外的崎岖道路上，步履艰难却又坚定不移地一步步前进着。古人有言：“欲穷千里目，更上一层楼。”在我们这里却是“欲穷亿年目，更上几层楼”了。

最后，我们再介绍一种饶有兴味而卓有成效的方法。为此，我们先从光谱线的“红移”谈起。