星星距离探测方法与结果

即使是远得无法分辨其中的单个恒星的球状星团或河外星系，天文学家也还是有办法对付它们的。

这时，可以根据星团和星系的大小来估计它们的远近。这种方法的基本原理，就是大家熟知的物体的“近大远小”。

比如太阳和月亮，它们在天空中看起来仿佛一样大，其实太阳的直径却是月亮的390倍。凑巧，太阳恰好又比月亮远了390倍，所以它们的视角径（即它们的圆面在天空中向我们张开的角度）便几乎相等，都是32′左右。从地球上看任何一个天体的视角径，总是同该天体与我们的距离成反比。换句话说，如图56，只要我们知道了一个天体的直径D（例如是多少千米或若干光年），又通过观测知道了它的视角径α，那么就可以通过下面这个再简单不过的公式算出它的距离r：

反过来，如果我们知道了一个天体的距离r和它的视角径α，那么又可以根据公式

计算出它的真直径D。(www.xing528.com)

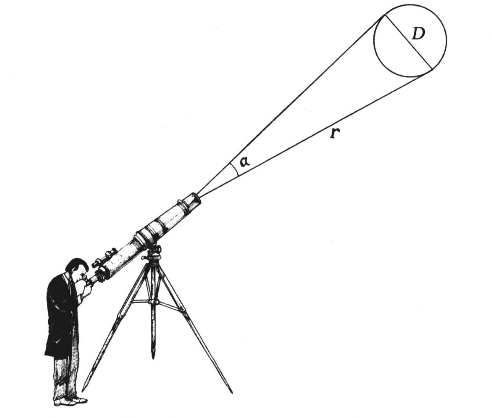
图56　天体的直径D、视角径α和距离r三者的相互关系

人们已经用前面谈到的一些方法（例如利用天琴RR型变星，利用新星或亮星等）求出若干球状星团的距离，并据此从它们的视角径求出真直径。结果是：球状星团的直径在20～150秒差距之间，平均直径约为80秒差距。倘若我们假定，某个距离未知的球状星团的直径也是80秒差距，那就可以从观测它的视角径推算出它的距离了。

不过，由这种方法得到的结果很不准确。这是因为：第一，如果一个球状星团的直径其实是20秒差距，而我们却认为它是80秒差距，这样直径就差了4倍，求出的距离也会差到4倍；第二，准确确定球状星团的视角径本身也很困难，因为一个星团中的成员星，越往星团的外围区域就变得越稀疏，到了星团的最外围就很不容易分清楚哪些星属于星团，哪些星不属于星团了。

由视角径求河外星系的距离，原理和方法都和球状星团的情况一样，但问题还要更严重些。由于大星系的直径（可达几万秒差距）要比小星系的直径（仅几千秒差距）大许多倍，因此用平均直径代替每个星系的真直径也就更不可靠了。星系的视角径也很不容易定准，它严重地受到拍摄星系照片时的观测条件的制约。

总之，这种方法只能粗略地推测星团和星系的距离。但是，它可以同用其他方法求出的距离互相比较、互相校验。