金星凌日：太阳视差测定方法的放弃

继卡西尼之后，又有法国天文学家马拉尔迪（Giacomo Filippo Maraldi，1665～1729年）于1704年由观测火星求得太阳的视差为10″左右，英国天文学家布拉德雷（James Bradley，1693～1762年）于1719年求得的结果为10.5″，拉卡伊于1751年求得10.2″。这些数值反倒不及卡西尼测得的9.5″精确。

英国天文学家哈雷（Edmund Halley，1656～1742年）早就提出，利用“金星凌日”的机会也可以测定太阳的视差。所谓“金星凌日”，就是从地球上看去，金星恰好投影在日面上，或者说，正好从太阳前面经过。在图17中，V代表金星，E代表地球，P1和P2是地球上的两个地方，S代表太阳。金星凌日时，从地球上的P1和P2同时进行观测，可以看见金星投影在日轮上不同的两个位置V1和V2，在金星移动的过程中，这两个点沿着两条平行的弦经过日轮。根据观测可以求得∠P1VP2的大小，据此根据开普勒第三定律，再运用一些简单的三角学知识，又可以推算出∠P1SP2的数值，倘若P1P2的直线长度（不是弧长而是弦长）正好就等于地球的半径，那么，∠P1SP2就正好是太阳的地心视差。

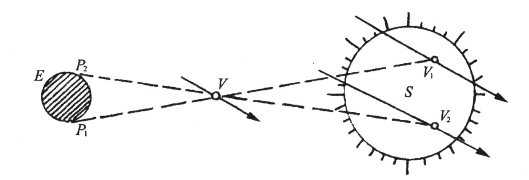
图17　利用金星凌日测定太阳视差

图中V代表金星，E代表地球，S代表太阳。金星凌日时，从地球上的P1和P2两处同时进行观测，可以看见金星投影在日轮上不同的两个位置V1和V2(www.xing528.com)

不过，哈雷本人却未能将这种方法付诸实践，因为金星凌日是不常发生的。那时，最近的两次金星凌日也须等待到1761年和1769年才会来到。哈雷虽然是一位长寿的天文学家，他活了86岁，但于1742年去世了。天文学家们为了观测1761年和1769年的金星凌日，事先作了充分准备。他们组织了不少远征队到世界各地去，希望在最好的条件下观测。可惜，许多复杂的因素都损害了观测的精密程度。1761年金星凌日时，各观测队求得的太阳视差数值差异很大：有的小到7.5″，有的大到10.5″。但是，天文学家们不屈不挠，重新努力，这使1769年的观测大有进步。这次观测之后一共发表了200多篇科学论文，其中大多数结果都在8.5″～8.8″之间。法国天文学家潘格雷（Alexandre-Gui Pingré，1711～1796年）综合分析了全部资料，于1775年公布了最后结果：太阳的视差为8.8″。这是一个非常准确的数字，可惜当时人们并不重视它。

再往后的两次金星凌日，发生在1874年与1882年。在等待它们到来之前，天文学家们有足够的时间重新研究过去的观测资料。最后，德国天文学家恩克（Johann Franz Encke，1791～1865年）于1824年发表了完整的讨论结果：太阳的视差为8.57″，由此算出地球至太阳的距离是153 000 000千米，这比实际情况多了3 500 000千米。直到19世纪中叶，恩克的结果一直为天文学界所公认。

最后，等待已久的1874年和1882年金星凌日终于来到了。天文学家们根据1874年的观测，求得太阳的视差在8.76″～8.91″之间。根据1882年金星凌日的观测，则求得它在8.80″～8.85″之间。美国天文学家纽康（Simon Newcomb，1835～1909年），又重新综合讨论了前两个世纪的4次金星凌日所取得的观测资料，于1895年最终得出：太阳的视差是8.797″。从1896年起直至1967年，国际天文学界都采用太阳视差值为8.80″。这些数字与此后公认准确的8.794″很接近。

这是一个不小的成就。然而，从那以后人们却完全放弃了用金星凌日来测定太阳视差的方法。因为一种更新颖的方法已经步入天文台的大门。