开普勒的三定律及其贡献

在16世纪，丹麦有一位第谷·布拉赫（Tycho Brahe，1546～1601年），他出身贵族家庭，起初学习化学和占星术。不过，他自幼也爱好天文学。他得到丹麦国王腓特烈二世的资助，在哥本哈根附近的汶岛上建了一座大型天文台，并命名为“天堡”。

第谷建造的天文仪器，在当时是最大最精密的。从1576年到1596年的20年间，他在“天堡”用这些仪器进行了大量观测。他是一位卓然超群的优秀观测家，然而却不是一位高明的理论家。他留下的最宝贵财富，便是丰富而精确的观测资料。当然，他对天文学也还有另外一些相当重要的贡献。

在他的保护人丹麦国王腓特烈二世去世后，第谷与新国王闹翻了。他被迫离开天堡，于1599年到达布拉格，担任奥地利皇帝鲁道夫二世的御前天文学家。第谷在那时结交了一位很有才气的青年，他的名字叫约翰·开普勒（Johannes Kepler，1571～1630年，图12）。第谷十分器重开普勒，身后将毕生积累的观测宝藏传给了这位年轻的助手。1601年10月24日，第谷与世长辞，开普勒继承御前天文学家的职位。

图12　发现行星运动三大定律的德国天文学家开普勒

开普勒幼年时体弱多病，因而损坏了视力。他17岁时进入蒂宾根大学基督教神学院攻读，1591年获得学位。第谷本人并不相信哥白尼的日心宇宙体系，但开普勒却不然。在天文学教授米切尔·麦斯特林（Michael Mästlin，1550～1631年）秘密宣传哥白尼学说的影响下，开普勒成了哥白尼的忠实信徒。1596年，开普勒写了一本书，名叫《宇宙的神秘》，承袭了毕达哥拉斯学派的“天球和谐”理论。书中虽然充满了神秘气氛，但仍清楚地表明他赞同哥白尼的日心宇宙体系。从此，开普勒便悉心探索诸行星轨道之间的数字与几何关系了。

第谷丰富的观测资料，到了开普勒手里才真正发挥了作用。开普勒利用这些资料，特别详细地研究了火星运动的轨道。经过无数次尝试和摸索，终于查明“火星沿椭圆轨道绕太阳运行，太阳处于椭圆焦点之一的位置上”。这便是开普勒第一定律的雏形。

开普勒发现，如果认为火星的轨道是圆形，则始终不能与第谷的观测数据相符，只有改用椭圆才能完全一致。这两者的差异，仅仅为8个角分。可是，正如开普勒本人所说：“就凭这8角分的差异，引起了天文学的全部革新！”

这里，我们顺便谈谈椭圆的一些奇妙特性。每个椭圆都有两个焦点，如图13中的F1和F2。椭圆上任何一点到两个焦点的距离之和总是相等的。所以，图13中的F1A1+A1F2=F1A2+A2F2=F1A3+A3F2=F1A4+A4F2=……利用这一特点，就有了一种简易的画椭圆的办法：只要用一支铅笔，一根细线，两颗图钉，按图13那样，将图钉按住细线的两端，用铅笔套在细线里绷紧了画个圈儿就行了。容易明白，两个图钉就是它的焦点。

椭圆还有一种奇妙的特征：倘若正好沿着一个椭圆的周界，面向椭圆内部布满镜子，那么放在一个焦点上的蜡烛或者灯泡发出的光，照到椭圆边界镜子上的任何一点后，就一定都会被反射到另一个焦点上。图13中，从一个焦点F1发出的光，射到A1，A2，A3……后，分别沿着A1F2，A2F2，A3F2……全部反射到另外一个焦点F2。

开普勒又发现，行星在近日点处运行得最快，在远日点处运行得最慢。但是行星与太阳的连线（这称为行星的向径）在同样时间里总是在椭圆内扫过相同的面积。

1609年，开普勒在他的《新天文学》一书内公布了他的头两条定律：

第一定律：行星绕太阳运行的轨道是椭圆，太阳在它的一个焦点上。(www.xing528.com)

第二定律：行星向径在相等的时间内扫过相等的面积。这条定律又称为“面积定律”。

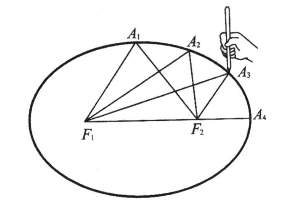
图13　从椭圆上的任何一点到两个焦点F1和F2的距离之和总是相等的

开普勒付出难以想象的艰巨劳动，在十几年内一直试图找出诸行星的公转周期与它们到太阳的距离之间的关系。他作了极为繁复的尝试和计算，遭到无数的失败之后，终于发现了行星运动的第三定律：

如果以年为单位计算行星的公转周期T，以天文单位来量度该行星与太阳的平均距离a（不难看出，它就是这颗行星轨道椭圆的半长径），那么周期T的平方就恰好等于平均距离a的立方。也就是说，对于每一颗行星都有：

或者，对于轨道半长径分别为a1和a2，公转周期分别为T1和T2的任意两颗行星，必定有（见表1）：

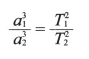
开普勒将这条定律发表在1619年出版的一本书中，他意味深长地将这本书取名为《宇宙谐和论》。就像第谷为开普勒发现这三条定律奠定了观测基础一样，开普勒的行星运动三定律也为英国大科学家牛顿（Isaac Newton，1642～1727年）后来发现万有引力定律筑起了攀登彼岸的金桥。

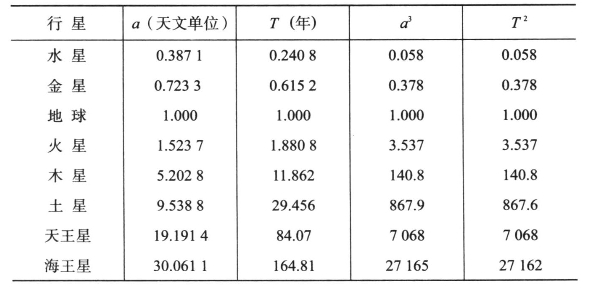
表1　行星轨道半长径a，公转周期T，以及a3和T2的数值

伟人开普勒虽然对天文学作出卓越的贡献（三定律便是这些贡献中较重要的一部分），但他的一生却扰攘维艰。为了生活，他不得不为人占星卜命。然而，他本人却并不相信占星术这门伪科学。1630年，他因经济极度困难而长途跋涉，去向日耳曼议会索取拖欠他的薪俸。同年11月15日，他在途中贫病交加悲惨地死去。