在图6甲中,需要测量子午线上相差1°的两点A、B之间的距离。但是,它们之间有山有树又有建筑物,再加上地球表面的弯曲,几千米外便是地平线,所以,A、B两地是不能互相直接看见的。测量必须迂回进行。
我们可以在图6甲中的a、b、c……各处立下标杆,组成一个“三角网”。立标杆的要求是:
(1)站在每一根标杆处都可以看到相继的两根:在A处可以看见a和b;在a处又可以看见b和c;在b处可以看见c和d……
(2)第一条直线Aa的长度可以用很准的尺直接量出来,它是整个测量工作的基础,因此称为“基线”。
测量就从第一个△Aab开始。我们知道,在一个三角形中只要知道一条边的长度和两只角的大小,就可以把另外两条边的长度求出来。这是平面几何学或平面三角学中最简单、最基本的问题。
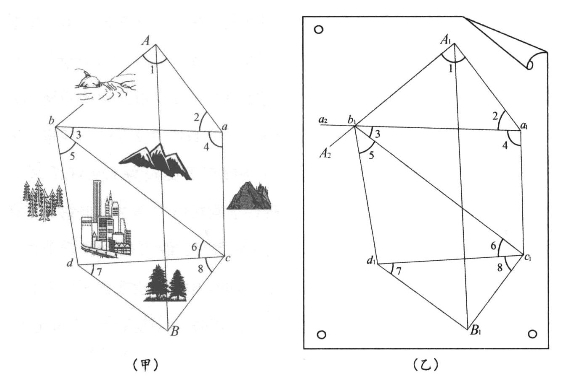
图6 大地测量中的三角网:
(甲)三角网,(乙)按比例缩小后作图
在△Aab中,Aa的长度可以直接用尺量出来;测量它的两个角也是轻而易举的。例如,可以在A点先用测量仪器瞄准a处的标杆,再将仪器转动一下进而瞄准b处的标杆,于是仪器转过的角度便是∠aAb(图6甲中用∠1来表示它)。同样,可以跑到a点,测出∠Aab(图6甲中用∠2表示)的角度大小。
于是,在△Aab中知道一条边Aa的长度和两个角(∠1和∠2)的大小,就立即可以算出Ab和ab的长度了。
当然,我们也可以换个方法来做。对于不喜欢计算的读者(对现代精密科学而言,懒于计算可不是好习惯),我们可以直接按比例作图。比如,拿一张白纸,在它上面随便点上一个点A1。从A1开始任意画一条直线A1a1(图6乙),要求它的长度比刚才量出的Aa(比如说,它是2千米吧)缩小若干倍——假定它缩小1万倍,那么A1a1的长度就是20厘米。再画一条通过A1的直线A1A2,使∠a1A1A2的大小就等于原先测量的∠1(例如,它是60°)。
接下来,我们再通过a1画一条直线a1a2,使∠A1a1a2等于原来测量的∠Aab,即∠2(例如,它是50°),直线A1A2和a1a2相交于b1处。现在,用米尺量出A1b1的长度(为16.3厘米),将它重新放大1万倍(这正是刚才作图时缩小的倍数),就知道Ab的实际距离是1.63千米了。同样,还可以知道ab的距离是1.84千米。
不过,当我们需要很高的精确度(例如,需要五位、六位甚至更多位的准确数字)时,作图的方法就不能适用了。这时,仍然必须进行严格的计算。(https://www.xing528.com)
总之,不论用什么方法,我们现在已经知道ab的长度。于是,测量工作可以转移到图6甲中的第二个△abc中进行了。在这个三角形中,现在已经知道ab的长度,我们将它作为基线,再测量一下∠abc(即图6甲中的∠3)和∠bac(即∠4)的大小,就又可以算出ac和bc之长。
接着,又在△bcd中,将bc作基线,再测出∠5和∠6的大小,便可得bd和cd之长。最后,在△cdB中,基线cd之长已经求得,测量一下∠7和∠8,就知道cB和dB的长。根据上面量出、测出和求出的所有角度和线段,按一定比例将整个图形画在纸上,便可以从图上直接量出AB的长度了。当然,我们再重复一遍,要想得到AB之间距离的精确数值,还得进行计算,仅仅靠作图是不够的。
这样测量的结果是:地球上子午线每一度的弧长是111.13千米,即从赤道到两极的距离是10 002千米。整个子午线的长度则为它的4倍,即为40 008千米。
200多年前,欧洲人进行的一些测量已经初步表明,地球并不是正圆形的,而是沿赤道方向稍“胖”一些,沿两极方向稍扁些。后来,这一结论又不断被种种更精确的测量所证实。
现代测量地球的形状和大小,除了用上述大地测量学的方法以外,还有所谓的“重力测量法”,以及利用人造地球卫星的“地球动力学测地法”。各种方法的联合使用,已经使测量结果的精确程度大大提高。目前国际上采用的数据是:地球的赤道半径a=6 378.137千米,极半径c=6 356.752千米。人们常常谈论地球的平均半径,它的定义是:
![]()
人们还经常用f表示地球的“扁率”:
![]()
也就是说,两极半径只比赤道半径短了1/300左右。
总之,人类目前已经相当精确地知道自己的摇篮——地球的大小和模样。而且,还一步步弄清它不仅是个扁球体,还更像一个“梨”状的旋转体。人造卫星的观测表明,地球赤道本身也不是正圆形的,而是一个椭圆。不过,赤道上的最大半径比最小半径只长了100米左右。因此,地球实际上更近乎是一个三轴椭球体。
总的说来,地球毕竟还是相当圆的一个大球。倘若把地球的直径缩小1 000万倍,做出一个模型,那么它的赤道就是一个半径为63.78厘米的圆,两极半径则是63.57厘米。用肉眼来看,根本不能发现它是扁的,你一定会以为它就是一个地地道道的大圆球呢。
现在,我们可以跨出自己的“家门”,开始测量离我们最近的天体——月球的距离了。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




