单向散列链的应用领域及技术介绍

6.2.1.1 单向散列链

单向散列链是在1981年针对安全口令验证而提出的一种安全技术［3］，并且作为一种重要的密码原语很快应用在其他领域，如微支付系统［4］、无线ad hoc网络中的数据安全传输［5］和流数据认证［6］等。单向散列链是对一个随机选择的种子S重复使用一个散列函数H（x），它具有以下性质：

•H（x）可以对任意长度的输入信息进行处理，并生成一个固定长度的消息摘要。

•对于给定的x，计算y＝H（x）容易。然而，对于给定的y，计算x＝H^－1（y）非常困难。

•对于给定的x，满足H（x′）≠H（x），求x′≠x在计算上是不可行的。

•找到任意x和x′，使得x′≠x和H（X′）＝H（X）在计算上是不可行的。

散列函数进行n－1次运算的结果分别表示为h₁，h₂，…，h_n，其中h₁＝H（h₂），h_i－1＝H（h_i），h_n＝S，1＜i≤n。h₁被称为链的顶端（tip）或承诺（commit^-ment），并且散列链的所有者能够以相反的顺序发布所产生的链元素。以这种方式，任何散列链元素可以保持秘密，直至其被发布，在收到一个链元素后，接收方可以容易地通过一个简单的散列运算验证其正确性。例如，接收者可以验证h_j是链的一部分，如果接收者知道h_i是链的第i个元素（i＜j），则接收者需要检查h_i＝h^j－i（h_j）。

单向散列链可以用来减少一系列消息的认证负担。但是散列链机制的主要问题在于其处理消息丢失的能力，而且传统的单向散列链具有固定的长度，但消息的数量随应用而变化。另外该方案需要已知认证的消息，这对大多数实时应用来说是一个很大的限制。(www.xing528.com)

6.2.1.2 TESLA认证协议

TESLA是能够容忍消息丢失的、高效的广播认证协议，具有通信和计算开销低的特点［1］，广泛应用于传感器网络中［7］。TESLA采用单向散列链，链元素是用来计算MAC的密钥。利用TESLA协议发送方按照接收方已知的预定的进度表发送数据包并确定用于计算散列链的承诺（commitment）。每个作为MAC密钥的散列链元素对应于一定的时间间隔。对于每个数据包，发送方给它附加一个MAC标签。基于发送方和接收方协商的密钥公开延迟时间表，使用散列链中下一个相应的MAC密钥导出此MAC标签。显然，在接收到数据包时，接收方无法验证该数据包的真实性。经过一个密钥公开延迟后，发送方公开了MAC密钥，当接收方验证了公开的MAC密钥确实是链中相应的元素后，就可以利用它验证该消息了。对于TESLA方案的一个要求是在节点之间进行松散的同步。该方案的缺点是延迟的消息验证使其容易遭受到拒绝服务（DoS）攻击，因为接收方必须缓存其接收到的尚未被认证的消息，如果恶意攻击者发送大量的消息，则可能会导致严重的安全问题，它可以很容易地消耗掉接收方的存储器，其结果是接收方必须丢弃以后到达的消息。［8－11］中给出了许多能够应对DoS攻击的基于TESLA的广播认证协议。为简单起见，本章不考虑防范DoS攻击。

6.2.1.3 布隆过滤器

布隆过滤器（Bloom Filter）是一个基于散列的空间高效的概率数据结构，用于查询一个大的集合项目，以确定一个给定的条目是否包含在集合中。它是通过将一组给定的数据项E＝｛e₁，e₁，…，e_n｝插入一个长度为m的比特串B＝（b₁，b₂，…，b_m）中，该串的各位初始都设定为0。如图6-1所示，k个独立的散列函数（H₁，H₂，…，H_k）被应用于集合中的每个数据项，以产生k个散列值（或索引值）（V₁，V₂，…，V_k），并且将位串中的所有相应位设定为1。当在Bloom Filter中查询一个条目时，假阴性匹配的情况是不可能发生的，也就是说，一个元素不可能被错误地识别为集合中的一个成员。但是假阳性匹配，即一个元素被指示为集合中的一员，但实际上不是的情况能够以预设的可接受的假阳性比率出现。因此，由于不存在假阴性，那么用Bloom Filter来确定一个元素没有实际存在比用来确定一个元素存在更有效。与其他数据结构相比，例如，二叉搜索树、数组或散列表，其占用的存储空间较少。

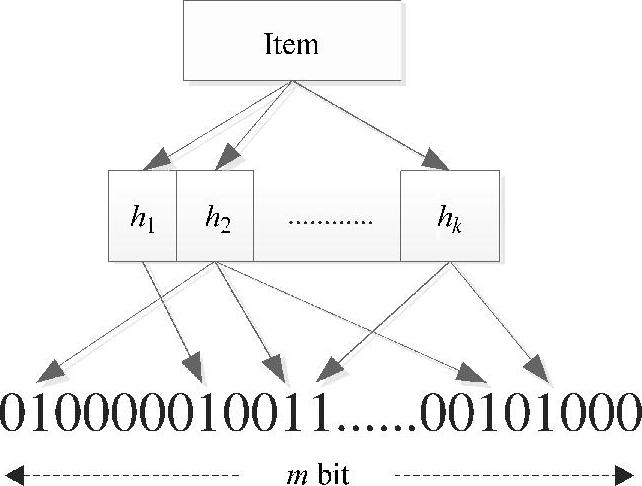
图6-1 一个m位标准Bloom Filter的例子。起始时过滤器比特串中各位均为零。集合中每个项目被散列k次，每个散列得到一个比特串的索引值，并将对应的位设置为1

Bloom Filter的主要特性概括如下［12］：①用于存储Bloom Filter的空间以及位串B的大小非常小；②查询一个元素是否在Bloom Filter中的时间是固定的，且不受集合中条目数的影响；③假阴性是不可能的；④假阳性是可能的，但出现的比率是可控的，但是较低的假阳性比率将需要更多的存储空间。作为一种表示一组元素的空间高效的数据结构，Bloom Filter已被广泛应用于Web缓存共享［13，14］、数据包路由［15］和差分文件简洁表示［16］等。