PCS策略的灵活性分析

在上面的匿名集分析中，假设所有车辆都改变了它们的假名，本节将采用简化的博弈论方法来证明PCS策略的可行性，即证明每辆车是可以通过在社交点改变假名实现其位置隐私的。

假设在社交点的匿名集尺寸ASS是N＝n＋1，其中n≥0，可以通过上面的匿名集分析估算出来。本节将研究所有车辆的隐私保护得到保护的合理场景。在社交点，每辆车V_j，1≤j≤N有两个可能的动作：修改（C）假名的概率为p_j，保持（K）假名的概率为1－p_j。如果V_j在社交点保持其假名，那么它被跟踪的概率为1。然后V_j的位置隐私丢失是不能更改的，并且这个行为的后果可以用标准化的位置隐私丢失－d_j表示，其中d_j∈（0，1）是V_j对位置隐私重要性的自评估。另一方面，当V_j在社交点修改了它的假名的同时，有其他车辆也做了相同的工作，那么匿名集尺寸将变为S。在这个社交点之后，V_j仍然被跟踪的概率为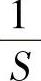。这种情况下，位置隐私的丢失将减少到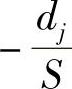。假设c_j∈（0，1）是V_j修改假名所需的正常的成本，那么这个行为的后果是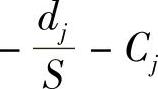。对于所有车辆，假设p_m是所有概率｛p_i｜1≤i≤N，i≠j｝的最小值，那么当V_j准备在社交点修改其假名时，它可以估算出平均匿名集的下限为

作为结果，车辆V_j的支付函数可以总结为

因为车辆V_j是合理的并且它的目标是保护它的位置隐私，因此V_j在社交点修改其假名的条件是：(www.xing528.com)

在采用的KPSD方案中，所有车辆自己生成和管理它们的假名。如果它们在旅行前能够生成足够多的假名，那么修改假名的开销会非常低。不过当n_pm为0时，式（4.23）将不成立，即当周围没有车辆修改假名时，V_j同样不修改它的假名。但是当n_pm大于0时，V_j总是可以减少开销c_j，使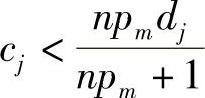。然后，V_j可以主动地在社交点修改它的假名。本节定义每个车辆V_j的位置隐私增益（LPG）函数为

LPG_j从p_m角度看是递增函数。当p_m＝1时，即所有车辆在社交点修改假名，LPG_j可以达到最大的收益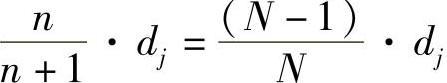。因为每辆车是合理地最大化其位置隐私收益，因此当它们都修改假名时是双赢的。作为结果PCS策略的灵活性在实践中是可以证明的。