在上面的KPSD方案中,在路上的每个车辆都持有一定数量的假名,然后按照算法3描述的应用PCS策略来保护位置隐私。为了从PCS策略中得到好处,本章开发了两个匿名集解析模型来分别研究在小的社交点和大的社交点上实现的位置隐私。


4.3.2.1 小的社交点的匿名集分析
如图4-5所示,当交通灯变红时,一队车辆将停在交叉路口[10],这时可以将交叉路口当成是小的社交点。假设当交通灯变绿时,所有的车辆同时改变它们的假名,然后交叉路口变成混合区。假设Sa是停在交叉路口的车的数量,那么期望的匿名集大小是(ASS)=Sa。匿名集尺寸ASS越大,在小的社交点提供的匿名性越强。本节针对ASS使用小的匿名集解析模型来研究小的社交点提供的匿名级别。
假设Ts=t,其中t=30s或60s,表示在交叉路口固定的停车时间。假设车辆到达(VA)交叉路口是一个泊松过程,ta是到达间隔,是具有均值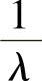 的指数分布。X是在周期Ts内车辆到达交叉路口的随机变量。那么基于参考文献[23]和[24],在Ts=t内,X=x的概率可以表示为
的指数分布。X是在周期Ts内车辆到达交叉路口的随机变量。那么基于参考文献[23]和[24],在Ts=t内,X=x的概率可以表示为
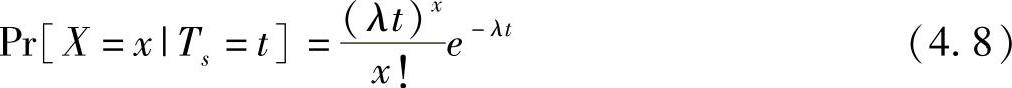
并且期望的X的数量可以通过下式计算:
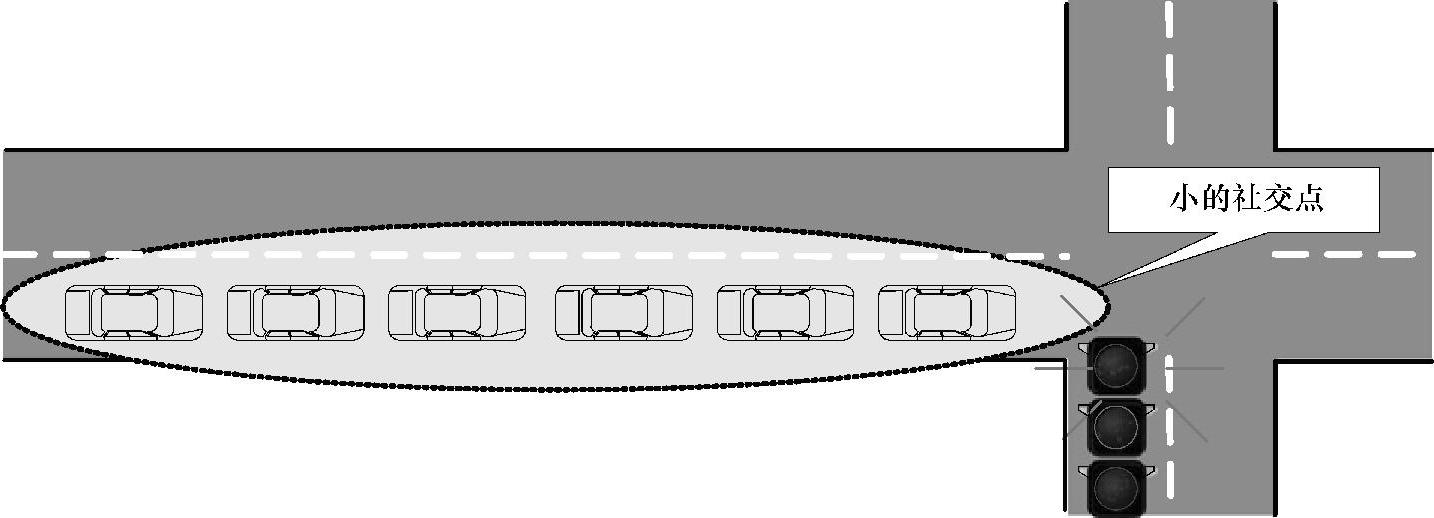
图4-5 在交叉路口进行假名修改
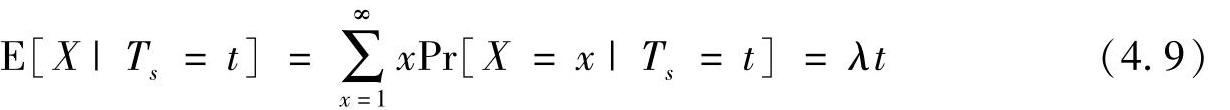
当交通灯变绿后,所有的车辆都会离开交叉路口,如果所有的车辆都服从PCS策略,那么匿名集尺寸ASS是
ASS=Sa=E[X|Ts=t]=λt(4.10)
4.3.2.2 大的社交点的匿名集分析
如图4-6所示,大的社交点可能是商场附近的免费停车场[19],因为停车场中通常会有很多的车辆,并且每辆车根据自己的意愿随机地离开停车场,如果所有的车在停车场内修改它们的假名并在随机时间内离开停车场,那么这样的一个停车场自然就变成了混合区。这种行为可以混乱到达车辆和离开车辆的关系,因此可以实现用户的位置隐私。
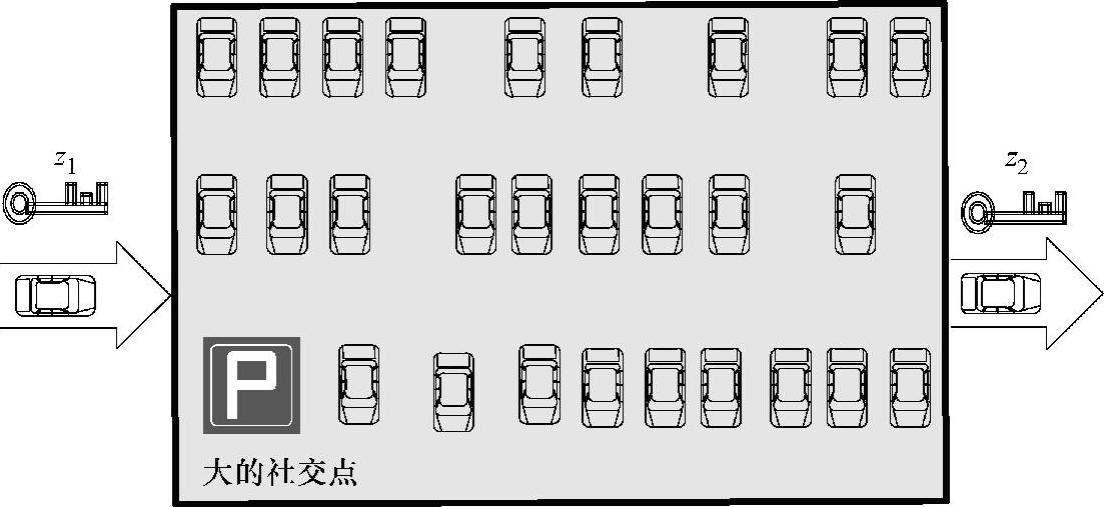
图4-6 在停车场的假名修改
假设Sa是车辆准备离开时停车场里的车辆数量,那么匿名集尺寸表示为ASS=Sa。本节针对ASS提出了匿名分析模型来研究在大社交点情况下能提供的匿名级别。
对于已经进入到商场附近停车场的车辆V修改假名,时间周期Ts是从商场开门的时间如8∶00到车辆V修改假名后离开时间,如图4-7所示,Ts是指数分布的,具有密度函数f(t)、均值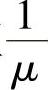 和拉普拉斯转换
和拉普拉斯转换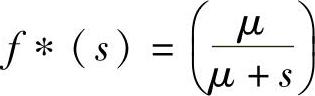 。在另一方面,其他车辆根据自己的意愿进入/离开停车场,例如驾驶人可以决定车辆停在停车场中的时间和时长。假设车辆到达停车场(VA)符合泊松过程,ta是到达间隔,ta是指数分布,均值为
。在另一方面,其他车辆根据自己的意愿进入/离开停车场,例如驾驶人可以决定车辆停在停车场中的时间和时长。假设车辆到达停车场(VA)符合泊松过程,ta是到达间隔,ta是指数分布,均值为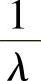 。另外车辆到达停车场到离开停车场的时间间隔tu假设有密度函数fu(·),均值
。另外车辆到达停车场到离开停车场的时间间隔tu假设有密度函数fu(·),均值 和拉普拉斯转换fu∗(s)。假设X是在时间周期Ts内到达停车场的随机变量,那么在周期Ts=t内X=x的概率可以表示为Pr
和拉普拉斯转换fu∗(s)。假设X是在时间周期Ts内到达停车场的随机变量,那么在周期Ts=t内X=x的概率可以表示为Pr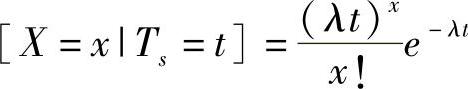 ,对于t≥0,可以得到:
,对于t≥0,可以得到:
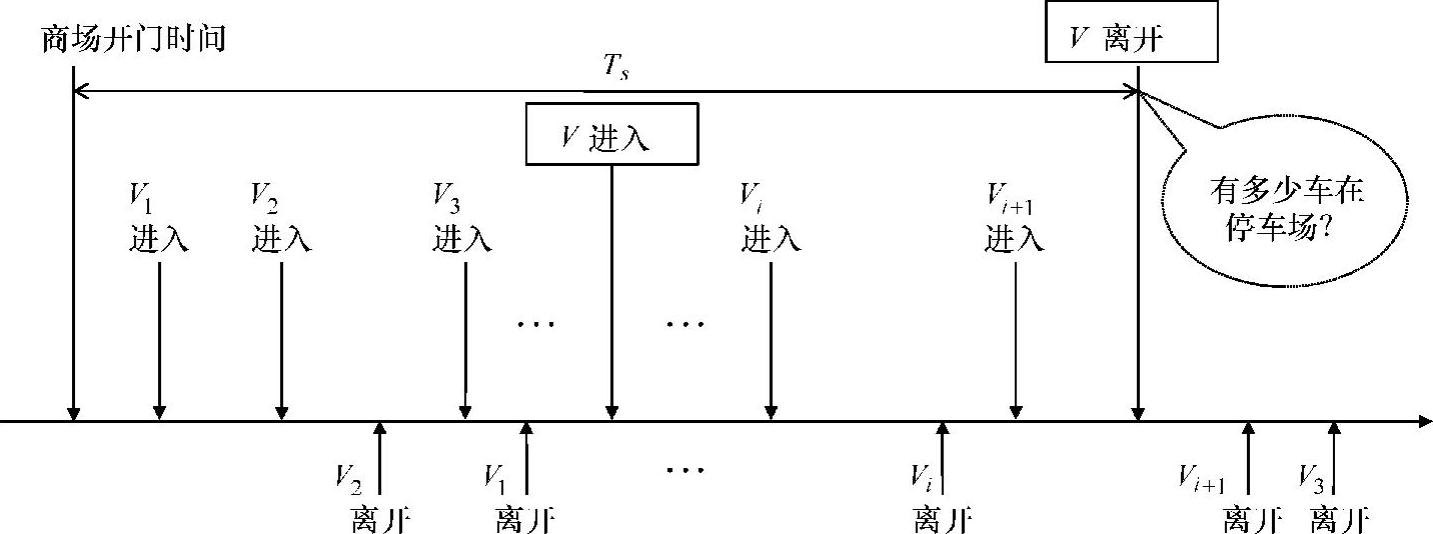
图4-7 时间图示(假设初始时在停车场没有车)
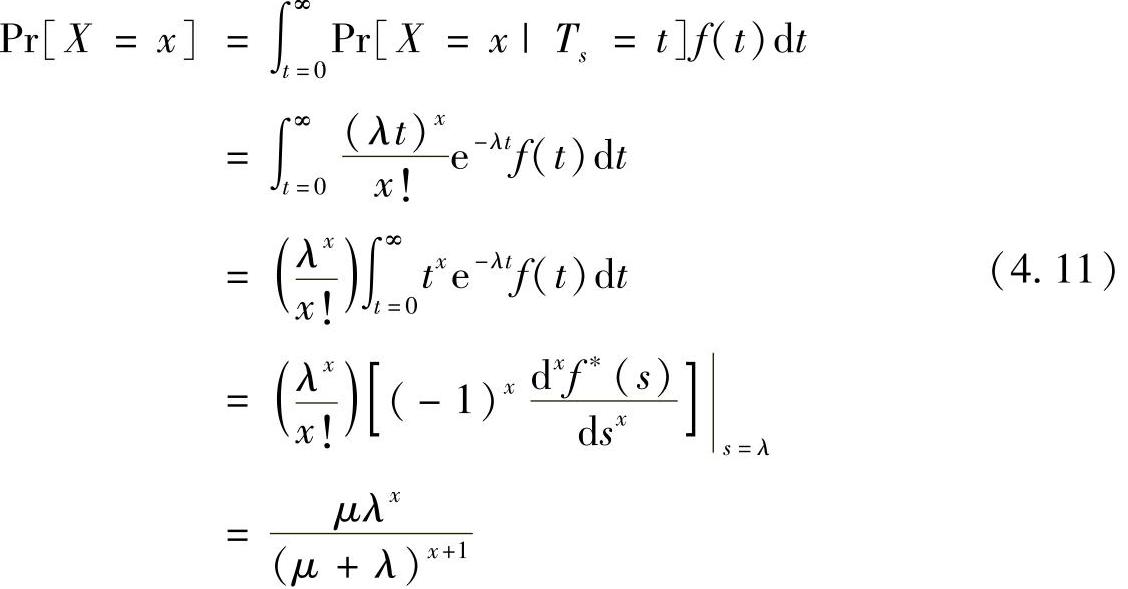 (https://www.xing528.com)
(https://www.xing528.com)
并且期望的X的数量可以按照下式计算
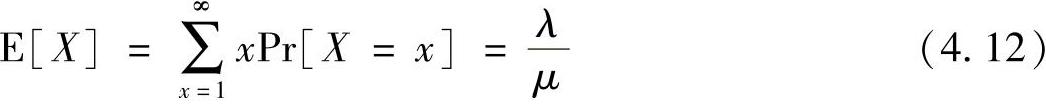
假设χ是车辆V到达停车场后到修改假名离开停车场的时间周期,因为Ts是指数分布的,针对分布χ的密度函数σ(χ)可以表示为
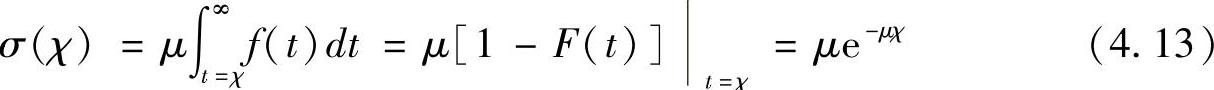
在Ts周期内,在车辆V离开前很多车辆可能会离开,即tu<χ,而其他车在V之后离开,即tu≥χ。假设Y是在V之前离开停车场的车辆数量,那么概率Pr[Y=y|X=x]可以表示为
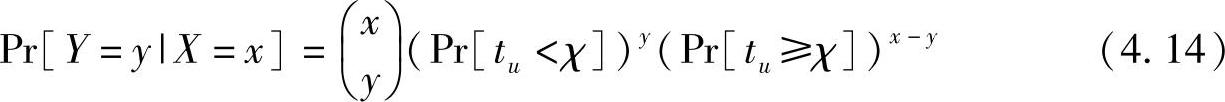
然后,概率Pr[tu≥χ]可以表示为:
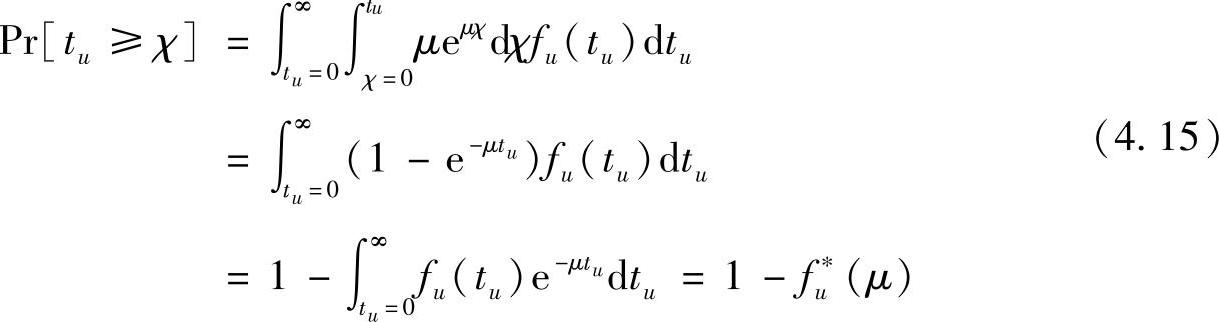
并且Pr[tu<χ]可以从Pr[tu≥χ]得到
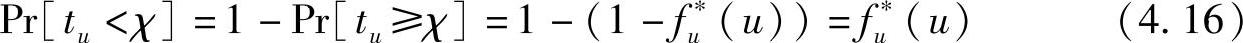
式(4.14)可以表示为
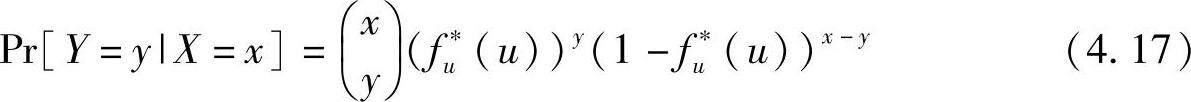
那么期望的Y的数量可以表示为
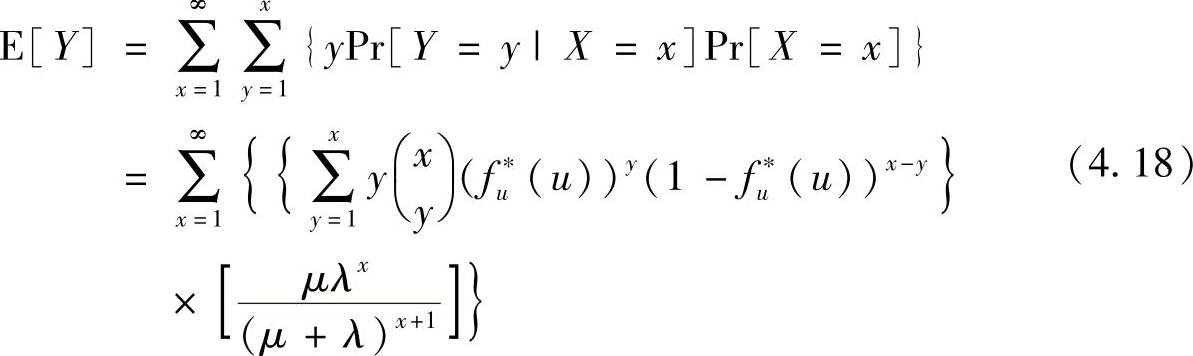
所以,针对车辆V的假名修改的期望的匿名集尺寸ASS可以表示为
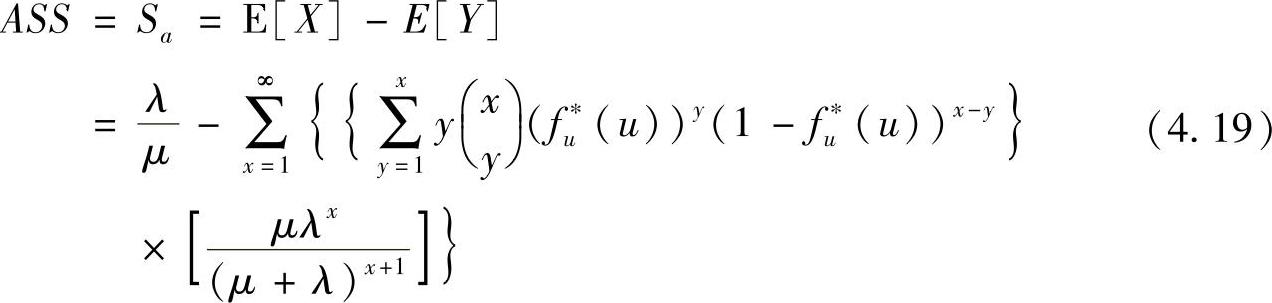
目前在很多真实场景[23]的建模中都使用了指数分布,因此本节假设tu符合指数分布。那么,拉普拉斯变换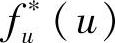 变成
变成

最后,Sanony可以表示为
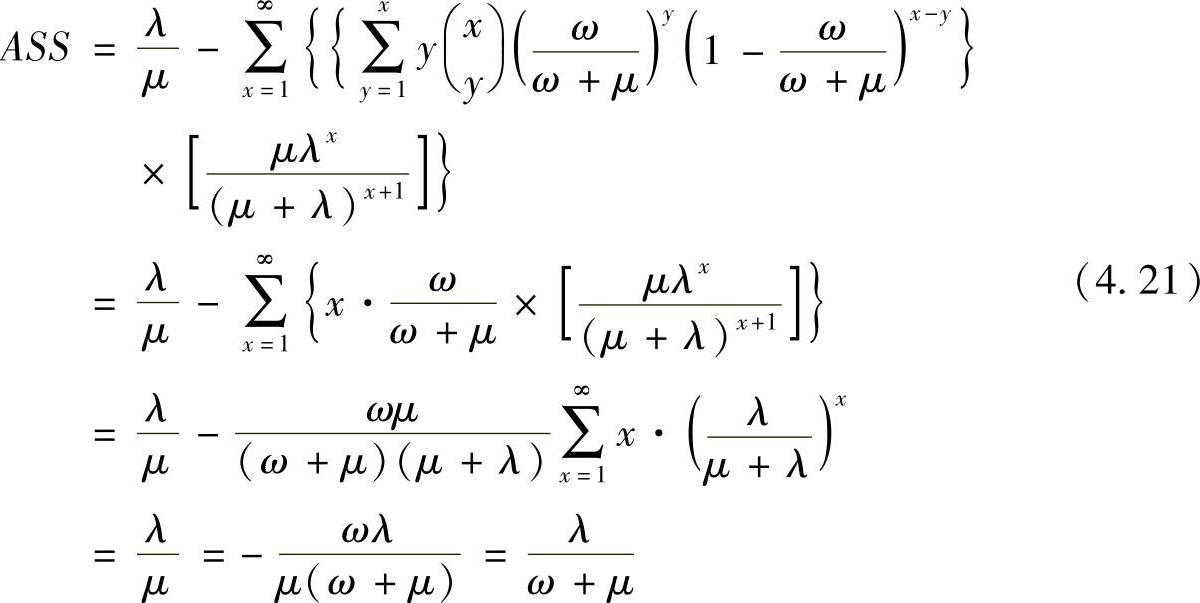
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




