建筑工程投标利润率计算方法

8.3.1　建立基础集合

确定投标目标组成的集合V、对目标因子的评价结论组成的集合W、利润率可取值组成的集合L、影响报价利润率的因素组成的集合S和所有报价利润率影响因素的指标强度组成的集合Y。

假定该集团在投标前已经对该项目的成本、利润、风险变化等因素进行了充分的预测，集团决策者的目的是通过计算本工程的最优报价利润率来拟定投标报价方案。依据本企业近年在鲁承建项目的统计资料表明该类工程的投标利润率介于4%—14%之间，即Lmin=0.04，Lmax=0.14，正常情况下预计利润率L应满足0.04≤L≤0.14，根据利润率等级差计算公式本文取利润率等级差值为0.02，将利润率划分为6个等级，l=6，得到的利润率计算数据见表8.10。

表8.10　利润率取值表

投标方认为本次投标的主要目标可以归纳为三个。首先最根本的目标是获得本项目的承包权（V1）；第二是拓展企业市场份额，巩固企业在山东建筑工程承包市场的地位（V2）；第三是尽量取得承包项目的企业利润最大化（V3）。

结合该项目面临的整个市场竞争情况和本企业资质情况分别定义三项目标分别所占的重要性强度为W1=1，W2=0.2，W3=0.3。投标方在报价时考虑影响报价利润率的因素为：潜在竟争对手的实力（S1）；公司内部编制施工组织设计的技术水平（S2）；建筑材料与所需资源的供应能力（S3）；本企业与有关社会部门的合作程度（S4）。四个影响因素的重要性强度分别为：Y1=1，Y2=0.7，Y3=1，Y4=0.8。即集合W=（1，0.2，0.3），Y=（1，0.7，1，0.8）。

8.3.2　确定影响度

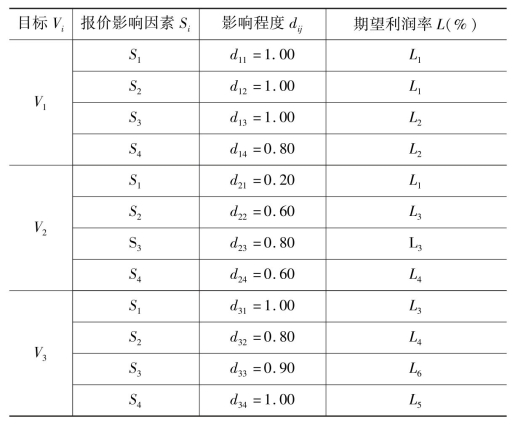
根据工程情况确定各影响因素对各目标的影响程度dij及在Vi上考虑因素Si所确定的期望最优利润率，如表8.11所示。

表8.11　报价影响因素对目标的影响程度及利润率对照表

影响度构成集合为式（8.4）所示：

8.3.3　V-S的模糊数学关系

计算目标V与报价影响因素S之间的模糊数学关系。目标Vi与影响因素Sj之间的模糊关系通过求解基础集合的笛卡尔积实现。

按照式（4.3）B×C={（1×a），（1×b），（2×a），（2×b），（3×a），（3×b）}和式（4.8）Gij=G（Vi，Sj）=Wi×Yj×djp（参见P58）的计算方法计算影响因素对应目标的影响度，

已知W=（1，0.2，0.3）；Y=（1，0.7，1，0.8）；

可以得到：

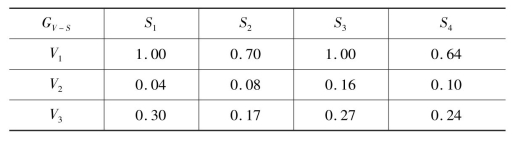
影响因素S1对报价目标V1的影响度G11=1×1×1×1；S2对V1的影响度G12=1×0.7×1×0.7；S3对V1的影响度G13=1×1×1=1；S4对V1的影响度G14=1×0.8×0.8=0.64；S1对V2的影响度G21=0.2×1×0.2×0.04；S2对V2的影响度G22=0.2×0.7×0.6=0.08；S3对V2的影响度G23=0.2×1×0.8=0.16；S4对V2的影响度G24=0.2×0.8×0.6=0.10；S1对V3的影响度G31=0.3×1×1=0.3；S2对V3的影响度G32=0.3×0.7×0.8=0.17；S3对V3的影响度G33=0.3×1×0.9=0.27；S4对V3的影响度G34=0.3×0.8×1=0.24；

所以计算出的目标与影响因素之间的模糊数学关系组成的集合为式（8.5）所示：

将式（8.5）列表表示V-S关系，见表8.12。

表8.12　目标与影响因素的模糊数学关系表

8.3.4　S-L的模糊数学关系

计算影响因素S与利润率L的模糊数学关系。影响因素Si与利润率Lp的模糊数学关系通过利率合适度构成的集合实现。

结合表8.11报价影响因素对目标的影响程度及利润率对照表中对应数据，分析如下：(www.xing528.com)

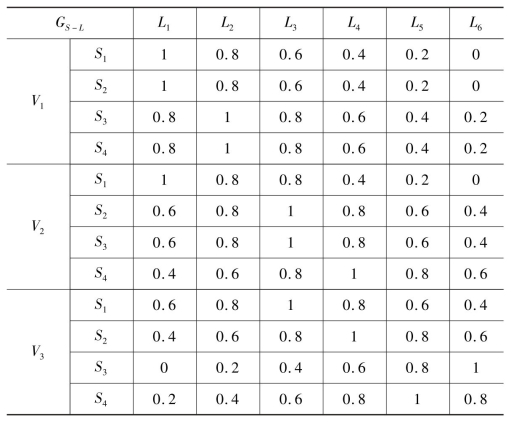
S1为目标V1的一个影响因素，当其发生作用时对应的最佳利润率为L1，则L1对应的最利合适度=1，根据距离依次递减0.2，可知L2的合适度为0.8，L3合适度为0.6，L4合适度为0.4，L5合适度为0.2，L6合适度为0。

S3为目标V3的一个影响因素，当其发生作用时对应的最佳利润率为L5，则L5对应的最利合适度=1，根据距离依次递减0.2，可知L4的合适度为0.8，L6合适度为0.6，L3合适度为0.6，L2合适度为0.4，L1合适度为0.2。

同理，通过以上方法重复计算可以得到目标的影响因素与对应利润率的模糊数学关系，如表8.13所示。

表8.13　影响因素与利润率的模糊数学关系表

8.3.5　V-L的模糊数学关系

根据本文第5章中介绍的模糊矩阵的合成运算方法，见式（4.2）、（4.5）、（4.9）、（4.10）、（4.11）、（4.12），可以计算得到目标V与利润率L的模糊数学关系。目标Vi与利润率L之间的模糊关系通过求解模糊关系Gij与利率合适度集合H的内积合成关系实现。计算过程举例如下。

GV1-L1=(1∧1)+(0.7∧1)+(1∧0.8)+(0.64∧0.8)=1+0.7+0.8+0.64=3.14

GV2-L1=(1∧0.8)+(0.7∧0.8)+(1∧1)+(0.64∧1)=0.8+0.7+1+0.64=3.14

GV2-L2=(0.04∧0.8)+(0.08∧0.8)+(0.16∧0.8)+(0.1∧0.6)

=0.04+0.08+0.16+0.1+0.38

GV3-L4=(0.3∧0.8)+(0.17∧1)+(0.27∧0.6)+(0.24∧0.8)

=0.3+0.17+0.27+0.24=0.98

同理，重复以上计算方法，可以求出所有目标V与利润率L的模糊数学关系值，并根据公式（4.12）可计算得到所有目标对某一利润率的综合影响值T′（Vi，Lp），如表8.14所示。

将表8.14的T′（Vi，Lp）数据进行标准化处理，按照前文确定的标准化公式（4.13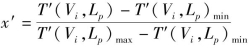）进行数据处理可得对应L1的T′（Vi，Lp）=2.79经标准T′（Vi，Lp）max-T′（Vi，Lp）min

化处理后结果为0.91，计算如式（8.6）所示：

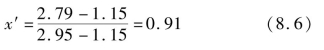
同理计算可得到其他所有T′（Vi，Lp）数据的标准化值，如表8.15所示。

表8.14　目标与报价利润率的模糊数学关系表

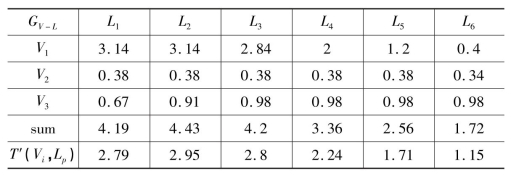
表8.15　T′（Vi，Lp）数据标准化处理结果表

结合表8.10、表8.14和表8.15并根据标准化的T′（Vi，Lp）最大值max{T′（Vi，Lp）}可以判断，目标的实现与利润率最为密切相关的利润率为L2，标准化值为1，max{T′（Vi，Lp）}=2.95，对应利润率为L2=6%；相关性最小的利润率为L6，标准化值为0，min{T′（Vi，Lp）}=1.15，对应报价利润率为L6=14%，这一点也验证了过高的报价利润率的不可取性。

按照式（4.14）将所有利润率进行模糊数学方法的综合计算，得到最优利润率为：

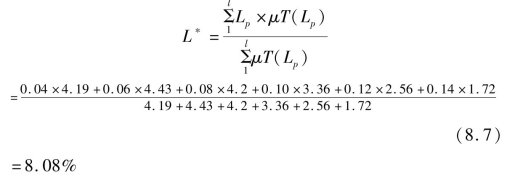
根据式（8.7）计算结果，本项目参与竞标的最优报价利润率为8.08%。该报价利润率符合建筑工程市场报价利润率5%—15%的范畴，也可以说明本计算模型具备一定的准确性。

这一报价利润率在后面的章节将作为已知量出现。