建筑工程投标报价求解模型

6.2.1　假设条件

要量化施工承包工程最优投标报价的存在性，首先要对承包工程投标报价的条件进行定性的约束限制，主要假设条件如下：

（1）存在承包工程项目M，项目M有一个认可的工程造价；

（2）投标商搜集资料购买标书等产生的投标成本计入工程总成本之中；

（3）业主一经提出工程的要求，就不再对相关工程要求作变化和退让，且统一选择最经济的方式对工程要求的实现进行实施；

（4）存在一个共同的市场法则，这一法则是业主方、承包方均乐意认可的，例如，认可共同的工程利润率等；

（5）工程承包商参与项目投标是以商业利益为出发点的，目的是寻求企业利润最大化，而非公益目的，也不存在低于成本报价的恶性竞标情况；

（6）这里所定义的最优利润报价并不是最终的投标报价，不包含风险费用在内，因此最终报价=最优利润报价+风险费用。

在设定了以上约束条件之后，本章的研究目的为求解项目M存在一个业主方和承包方均能乐意接受的最优利润报价。

6.2.2　求解过程

设：工程实际成本为C，业主方计算的标底为Cbp，工程的业主方可以接受的投标人最高投标报价利润率为θ，所以θ也是投标人的最优报价利润率，风险费用为F，承包方参与投标的报价为p，中标概率为G，期望收益为E（M）。

站在项目承包方的角度，对待一个项目，承包方有两个心态：首先是参与投标是以商业利益为出发点的，目的是寻求企业利润最大化。企业试图获利大需要进行高投标报价，即p越大获利越多。但p越大的同时，中标的可能性也越来越小，因为业主方不会乐意使得投资更多地变为承包方的利润；第二，承包商在能保证获利空间的基础上希望中标的可能性G越大越好，但G的增大必然意味着投标方给出的报价不可能过高，这样项目的获利空间就会减小，如果报价低于工程的成本价就会出现亏本的情况。可见中标概率G的大小、报价p的高低之间必然存在一个令业主方和承包方均满意的平衡点，即标底。当报价与标底差距越小，则越符合业主方的期望，当报价恰好等于标底，中标概率则为1。所以，概括承包商以上的两种心态，建立数学计算公式，具体为：

（1）为合理表述中标概率与投标报价的关系并简化计算，可将获取工程项目M的概率定义为：

其中σ为常数且0≤σ≤1，它的取值取决于投标方在竞争中的优劣程度，为计算简便，这里取σ=1。

（2）中标方在项目M上获取的利润大致为投标报价与工程实际成本的差额。即

（3）期望利润值为：

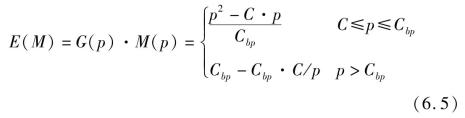
站在业主方的角度，业主方不会乐意投资更多的变地承包方的利润，所以只允许一定的利润率，即不会认可过高的投标报价p。所以，当p大于某一界限值时，G=0。这一界限值可以用最优报价利润率θ来确定，即当p＞（1+θ）·C时，业主方不接受投标者中标，中标概率G=0。

因此，可以综合业主和承包商的几种心态，建立如下项目投标报价的中标概率和期望利润值计算公式：

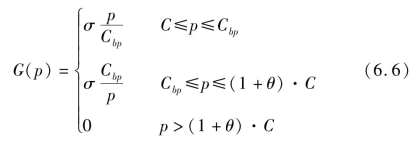(www.xing528.com)

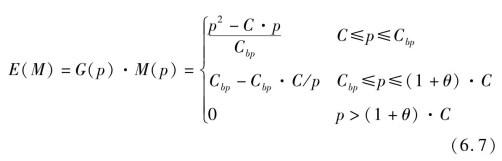
其中M（p）=p-C为工程的实际利润。

图形表示如图6.3、图6.4所示。

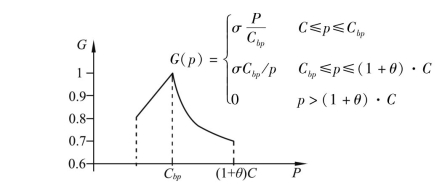
图6.3　中标概率计算曲线

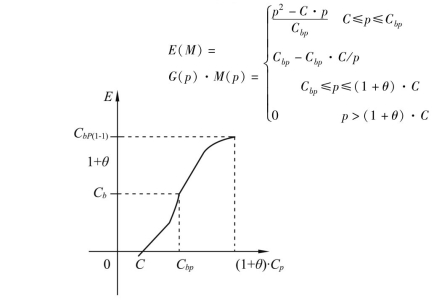
图6.4　期望利润值计算曲线

对E求导得：

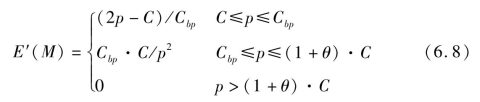
山东科技大学博士学位论文施工企业最优利润报价与报价区间求解模型公式曲线如图6.5所示：

由图6.4、图6.5可以看出，当C＜p＜（1+θ）·C时，E′（M）＞0恒成立，E（M）单调递增。

即企业的最优利润报价为：

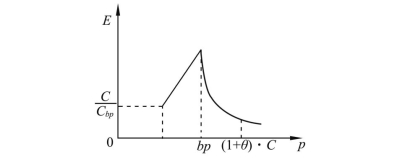
图6.5　期望利润值求导曲线

所以E（M）在区间上可以取得最大值，即当p=（1+θ）·C，E（M）取得最大值，为：

由以上证明步骤得结论：项目M具有最优利润报价为p=（1+θ）·C时，期望收益为θ·Cbp/1+θ。

需要特别注意，工程成本指的是针对特定工程项目的投标企业的实际成本，即便是同一工程项目，工程成本这一概念对不同的投标人也是不同的。项目的工程成本与投标企业的管理能力、技术水平及原材料的市场供应情况和企业的人工机械定额密切相关，并且业主方计算的工程造价和招标标的需严格保密，在递交投标文件截止时间之前不会让投标人在竞标过程中知道，即C和Cbp是未知的，所以承包商在计算最优报价时只能对C和Cbp做估计值，表示为C′和C′bp。C′的估算方法取决于企业的实际技术和管理水平，而C′bp的确定取决于市场平均利润率。

由最大期望收益计算公式（6.10）可以看出，计算中最关键的部分是报价利润率θ的确定。在本文第4章研究了最优投标利润率的计算方法，在本章6.1.2中也引用了前人对θ取值的研究结论，可以说明θ的取值是可以确定的。但不可避免，θ的取值还要具体情况具体分析，要视建筑市场是否处于饱和状态等其他因素进行综合确定。