建筑工程投标决策模型研究成果

4.3.1　模型假设

（1）施工企业可以根据所承建项目的统计资料确定某一类型项目的投标利润率取值范围；

（2）结合该项目面临的整个市场竞争情况和本企业资质情况，施工企业决策层能够确定的竞标目标及各分项指标的权重；

（3）通过分析工程实际施工企业能够确定报价影响因素，对不同目标产生的影响及在目标Vi上考虑因素Si所确定的期望最优利润率；

（4）企业决策层可以判断某一报价影响因素对利润率的影响程度的评价分值，介于0～100之间；

（5）影响因素Si与利润率的模糊数学关系通过利率合适度构成的集合实现。最优利率合适度可以根据投标决策方的效用观点确定，其他的利率合适度按照与最利合适度的距离以此递减利率等级差值，并且等级差值一致。

（6）本章报价利润计算方法取投标报价利润=工程成本×利润率，适用于总承包工程投标报价。

4.3.2　建立基础模糊集合

求解模型需建立以下基础集合：

根据图4.1所示，设定投标目标组成的集合为V=（V1，V2，…，Vm）；

结合该项目面临的整个市场竞争情况和本企业资质情况，经查阅相关文献，由企业决策层确定的各分项指标组成的集合为W=（W1，W2，…，Wm）；

影响因素组成的集合为S=（S1，S2，…，Sn），其指标强度组成的集合为Y=（Y1，Y2，…，Yn）。

设定利润率指标具有最大值Lmax和最小值Lmin，即利润率满足Lmin≤L≤Lmax，将利润率L分为l个等级，令利润率等级差，设Lp=Lmax+（p-1）Z，p=1，2，…，l为等级值，构成利润率评语组成的集合X={Lp}；

4.3.3　确定影响度

贴近度是广义的模糊集合中的概念，本文在分析投标报价利润率的求解方法时将各因素之间的贴近度直观地称为影响度。

如果规定djp为因素Sj对利润率Lp的影响程度的评价分值，分值介于0～100之间。

djp=0表示Sj对利润率Lp的影响程度为0，djp=100表示Sj对利润率Lp有完全的影响。

在取值后按照计算公式转化为[0，1]区间上的数值。

影响度构成集合为式（4.7）所示：

4.3.4　建立V-S-L模糊数学关系

（1）V-S的模糊数学关系

目标Vi与影响因素Sj之间的模糊关系通过求解基础集合的笛卡尔积实现，具体求解方法见式（4.3）（参见P59），V-S的模糊数学关系表示为Gij，

这一关系表示一个影响因素对于实现一个目标时对利润率的影响程度。这里计算并不是传统意义上的矩阵计算，而是矩阵对应元素的笛卡尔积所组成新的矩阵。计算结果构成的集合即为目标Vi与影响因素Sj之间的模糊数学关系集合。(www.xing528.com)

（2）S-L的模糊数学关系

影响因素Si与利润率Lp的模糊数学关系通过利率合适度构成的集合实现。

hijp表示在给定影响因素Si和目标Vj的条件下Lp最合适的利润率取值，称为最优利率合适度。最优利率合适度往往根据投标决策方的效用观点确定目标，其他的利率合适度按照与最利合适度的距离以此递减利率等级差值。

例如，假设利率等级差值为0.2，如果投标决策者认为L3是最优利润率，即对应L3的利率合适度=1，称为最优利率合适度，根据与L3的距离，L2和L4的利率合适度分别递减0.2，为0.8，L1和L5的利率合适度为0.6，这里的利率合适度其实是模糊数学理论中的贴近度。

（3）V-L模糊数学关系

目标Vi与利润率L之间的模糊关系通过求解模糊关系Gij与利率合适度集合H的内积合成关系实现。内积合成的计算方法见式（4.2）和式（4.5）（参见P59、P60）。

设H=（hijp），模糊关系G和H的合成计算式表示为式（4.9）：

通常情况下此合成运算的目标值为最值，即计算最大值或最小值，可以将此定义描述为式（4.10）：

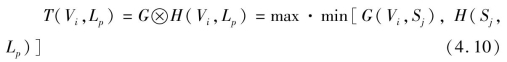
式（4.10）表示合成运算的目标值包含最大值和最小值。

在投标报价中，为概括在目标和利润率之间每一个最小的模糊数学关系，需要将每一个合成目标值设定为最小值，即求解集合的内积关系，然后求解所有最小值的合成关系之和，即可以定义合成运算方法表示为式（4.11）：

（4）V-L综合影响值

为计算Lp的取值，必须考虑全部的报价目标对利润率Lp的整体影响，假设t′（Vi，Lp）代表第i个目标对第p个利润率的影响值，T′（Vi，Lp）代表全部目标对利润率的综合影响值，则有：

其中ΣWi为分项指标值之和。

为便于比较，将计算出的T′（Vi，Lp）值进行标准化处理，可以得出目标的实现与利润率最为密切相关的组合。标准化算法按照下式（4.13）进行：

设标准化后数据为x′，则：

max{T′（Vi，Lp）}所对应的Lp即为最优利润率的取值，用L∗表示，如式（4.14）所示。最优利润率为：

其中μT为t′（Vi，Lp）中对应值，按照最优利润率可以筛选最优的报价方案。