瞬态操纵稳定性仿真与试验：车辆动力学与空气悬架系统研究

由于试验条件和试验时间的限制，单移线瞬态操纵稳定性道路试验只是进行了50 km/h和70 km/h两种车速，很难对该车的移线瞬态操纵稳定性有全面的了解，而且一些危险的高车速工况下车辆试验是难以进行的。因此本书基于所开发的低地板城市客车的虚拟样机，建立了最优曲率驾驶员模型[126]，对该款低地板城市客车的瞬态操纵稳定性进行了基于实车试验的仿真研究。

汽车的转向运动，简单的服从“Acklman几何关系”，即汽车的轨迹曲率与转向盘转角成正比，其表达式为

现设汽车在一个预定的路线上行驶，轨道中心线的方程为f(t)，并设在所考察的瞬间时刻t，汽车具有的即时状态为y=y(t)，。假设驾驶员的目光集中于前方一点处，即“单点预瞄”，当驾驶员向前预视一个距离d时，相应的“前视时间”为T=d/v，驾驶员前视点的横向坐标为f(t+T)。此时若他选择一个转向盘角度δsw，则对应的汽车轨迹曲率为1/R，横向加速度为。这样，经时间T 之后，在时刻t+T 汽车的横向位移为

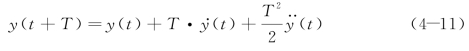
根据最小误差原则，驾驶员总是希望选择一个最优轨迹曲率1/R*，使得汽车在走过距离d(经时间T)后，其横向位置y(t+T)与该处的预期轨道坐标f(t+T)相一致。

由式(4-11)并考虑路径方向角不大时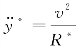，最优横向加速度和最优曲率为

由式(4-10)可得最优转向盘转角为

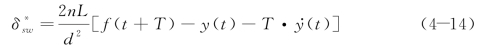
最优曲率驾驶员模型的物理意义为：驾驶员根据前方轨道信息f(t+T)和汽车的即时状态y(t)与，及其对车速v与前视时间T 的判断来确定一个最优的轨迹曲率1/R*，而后由转向系传动比n 和轴距L 来确定最优转向盘转角。驾驶员用这个方向盘转角操纵汽车，使它产生横向加速度、横向速度和横向位移y(t)。

实际情况中，由于存在驾驶员反应滞后的现象，在实际方向盘转角与理想方向盘转角之间有滞后环节。现设驾驶员的神经反映滞后时间为td，驾驶员手臂与汽车转向盘惯量等的操纵反映滞后时间为Th，则系统中与δsw 之间的理想环节“I”变为e-tds·。另外，在一般情况下，汽车并不是一个理想系统，尤其当汽车的转弯运动比较剧烈时，汽车本身的动态响应是不可忽略的，故系统中车辆传递函数(s)将不是，而是

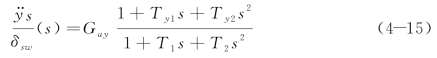
其中，Gay 为横向加速度稳态增益；Ty1，Ty2，T1，T2 为传递函数常系数。

这时驾驶员由判断理想曲率1/R* 进而断定理想转向盘角度所对应的传递函数也不是系统中的n L，而是更一般的传递函数C(s)：

其中，C0=v 2/Gay，Tc 为校正时间常数。

考虑到上述实际情况的驾驶员模型的物理意义为：驾驶员依据道路信息f(t)，经过预瞄e Ts，判断出预瞄点的位置y(t+T)并作为系统的有效输入，同时根据汽车的即时状态及其前视时间T 来判断汽车理想的横向加速度 及最优曲率1/R*，进而通过驾驶员校正环节C(s)得出理想方向盘转角，再经过驾驶员滞后环节e-t d s/(1+Ths)，求出驾驶员施加于方向盘的实际转角δsw，最后通过汽车本身的动力学特性/δsw(s)，使汽车产生横向加速度，横向速度及横向位移y(t)。

驾驶员模型是在Matlab/Simulink环境下编译的，运行该程序可以输出不同车速下的单移线和双移线的最优驾驶员反应，对于低地板城市客车虚拟样机而言是转向角输入；在低地板城市客车的虚拟样机模型中，定义相应的输入变量，接受控制系统变量并将其赋予转向轮转角变量，定义输出变量，输出所需参数。需要注意的是在仿真过程中，驾驶员模型的仿真时间与步长要与虚拟样机的仿真时间与步长相吻合，保证Matlab与ADAMS之间进行的联合仿真是实时的，运行时的每一步仿真都要在模型之间进行相应的数据交换与计算。

对于如图4-23所示的单移线道路，图中横坐标轴代表汽车前进方向的位移(时间)，纵坐标轴代表汽车侧向位移的距离，其道路输入函数f(x)表示为

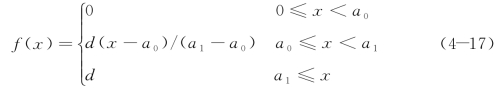
这里认为原点是汽车行驶的起始位置。在进行人-车-路闭环系统的侧向动力学仿真时，a0 应大于驾驶员的预瞄距离，即a0≥uT，这里u 为车速，T 为驾驶员的预瞄时间。若a0≤uT，则道路输入函数实际上是个阶跃函数。故a0 应当取得比可能的预瞄距离大一点。

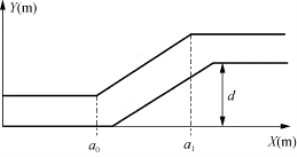
图4-23 单移线操稳性实验道路

由于图4-23中的单移线道路在折点处方向突变，这对汽车来说是不可能实现的，因此驾驶员心中理想的目标轨迹应该是最接近于这条折线的低阶曲线。最简单的处理方法就是用三阶曲线拟合，约束条件为折点处道路函数及道路函数的一阶倒数连续。拟合后的道路输入函数为

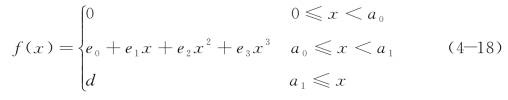
式中：

e0=(3a1-a0)d/(a1-a0)3，e1=-6a0a1 d/(a1-a0)3；(www.xing528.com)

e2=3(a0+a1)d/(a1-a0)3，e3=-2d/(a1-a0)3。

考虑到车速的变化会带来驾驶员预瞄时间的变化，从而造成不同车速下对同一车辆的评价结果会不同。这样就会使得评价结果不能真正反映车辆的整体性能。为了消除车速对评价结果的影响，在研究过程中采用了时间域的单移线道路模型。

将x=ut代入上式，有

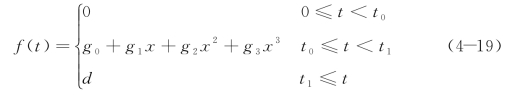
式中，t0=a0/u，t1=a1/u，g0=e0，gi=eiu，(i=1，2，3)。

对于如图4-23所示的单移线道路，虚拟样机仿真的转向输入采用两种方式：驾驶员模型输入和模拟试验驾驶员实际输入。车速为50 km/h时的转向轮转角输入如图4-24所示，车辆侧向加速度响应和侧倾角响应分别见图4-25和图4-26。

从以上分析结果可以看出，当按照道路试验的转向轮转角输入虚拟样机时，虚拟样机的侧向加速度响应和侧倾角响应与道路试验的数据基本吻合，有力的证明了虚拟样机模型的高精度；当转向轮转角输入驾驶员模型时，虚拟样机的响应数据与试验数据在数值上有一定的差别，但其基本趋势是一致的。同时，从以上数据还可以看出该低地板城市客车具有较好的瞬态响应能力，巡航车速下的单移线侧倾角和侧向加速度保持在一个较低的水平。

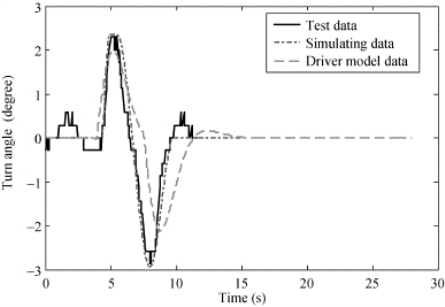
图4-24 转向角输入仿真与试验数据比较(50 km/h)

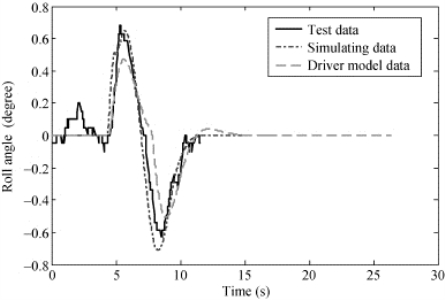
图4-25 侧倾角响应仿真与试验比较(50 km/h)

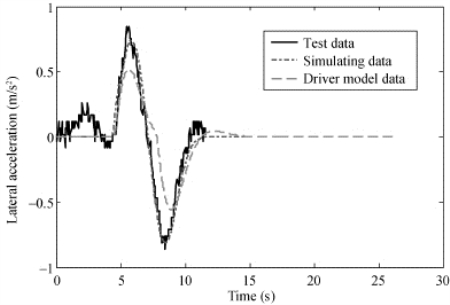
图4-26 侧向加速度响应仿真与试验数据比较(50 km/h)

实车道路试验由于各种资源的限制，试验车速仅取在50 km/h的巡航车速和较高车速70 km/h，下面本书利用所建立的驾驶员模型和虚拟样机仿真系统进行高速工况下的瞬态转向特性分析，仿真最高车速达到100 km/h。本车的设计最高车速为75 km/h，而且从安全性考虑，试验车速一般不会超过70 km/h，所以本书进行高速情况下的瞬态操纵稳定性分析可以弥补道路试验的不足。图4-27显示了不同车速下的转向轮转角输入，图4-28和图4-29分别显示了各种车速下车辆的行驶路线和车身的侧向加速度曲线。

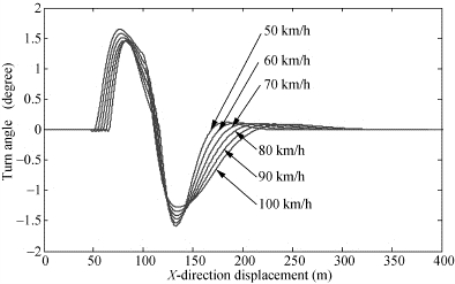
图4-27 不同车速下转向轮转角输入

图4-28 不同车速下车辆的行驶轨道

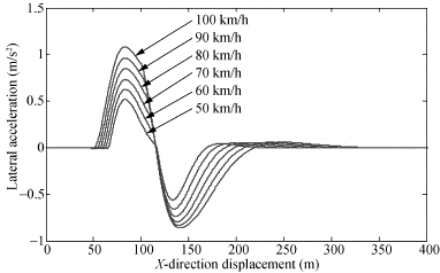
图4-29 不同车速下车辆的侧向加速度

从图中可以看出，随车速的增高，跟随同一轨道所需的大客车转向轮的转角就越大，车身的侧向加速度越大，车辆行驶的轨道距预定轨道越远。当车速达到100 km/h时，车辆的侧向加速度峰值在1.2 m/s2 左右，保持在一个较低的水平，表明该低地板城市大客车具有较好的稳定性，主要体现在以下两点：

(1)重心较低。低地板城市客车的地板高度最低处距地面37 mm，整个地板只有后部安装发动机处较高，有效地降低了整车重心的高度。

(2)空气悬架的非线性特性增加了整车的侧倾刚度。

从以上的仿真分析中还可以看出，最优曲率驾驶员模型输出的方向盘转角虽然与试验驾驶员操纵转角是有一定的差异的，但是还是比较合理地满足了本书的研究需要，原因主要有以下几点：

(1)驾驶员的方向盘操纵输入具有一定的随意性：同一路面不同的驾驶员的反应固然是不一样的；即使是同一路面，同一试验内容，同一驾驶员，二次乃至多次试验之间的反应也是不同的，因此试验条件下驾驶员的反应不具有否决权。

(2)驾驶员模型输出的转向轮转角是理想状况下的最优转角，只要试验条件相同，那么模型的输出都是一样的，不会出现随机现象。而且从图中可以看出，模型的输出转角与试验条件下驾驶员的输出趋势是一致的，所以认为该驾驶员模型是满足本书研究要求的。

综上所述，移线试验与仿真数据显示该车具有较好的路面跟随能力，瞬态操纵稳定性比较高。车辆设计最大车速为75 km/h，在50 km/h巡航车速下进行移线行驶时，侧向加速度保持在1 m/s2 以内，侧倾角不超过1°，行驶比较平稳。