车辆动力学空气悬架系统研究成果

模态分析可以确定零部件的振动特性——固有频率和固有振型，ANSYS软件中的模态分析是线性分析，任何非线性特性，如塑性、大变形和大应变单元，即使定义了也会被忽略。

在有限元模型的建立过程中，横向稳定杆近似为线性结构，除考虑受重力和其他静载荷外，还要考虑分布于体积内的惯性力和阻尼力。对于N 自由度线性系统，其运动微分方程为

式中 [M]—— 质量矩阵；

[C]—— 阻尼矩阵；

[K]—— 刚度矩阵；

{F(t)}—— 激励力向量；

{X}——节点位移响应向量。

其中质量矩阵[M]是正定矩阵；刚度矩阵[K]对于无刚体运动的约束系统是正定的，对于有刚体运动的自由系统则是半正定的；当阻尼为比例阻尼时，[C]为对称矩阵；{X}及{F(t)}分别为系统各点的位移响应和激励力向量。

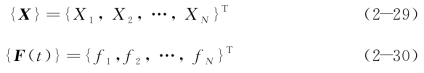
方程(2-28)是用系统的物理坐标{X}，和描述的运动方程组，在每一个方程中均包含系统各点的物理坐标，因此是一组耦合方程。当系统自由度数很大时，求解比较困难。模态分析法就是以无阻尼系统的各阶主振型所对应的模态坐标来代替物理坐标，使微分方程解耦，变成各个独立的微分方程，从而求出系统的各阶模态参数。

对式(2-28)进行拉氏变换，可得

式中，s=σ+jτ，为拉氏变换因子；

，为响应的拉氏变换；

，为激励的拉氏变换。

式(2-31)又可以写为

式中，Z(s)=s 2 M +s C+K，为N×N 阶位移阻尼矩阵。

Z(s)的逆矩阵为传递函数矩阵H(s)：

对线性时不变系统，其极点在复平面左半平面，因此可将s 转变成jω，得出在复数域中的阻尼矩阵及频响函数矩阵。

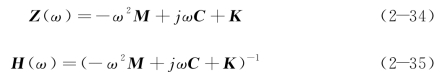
此时，系统的运动方程为

由振动理论知，对线性时不变系统，系统的任一点均可表示为各阶模态响应的线性叠加，对第m 点的响应有

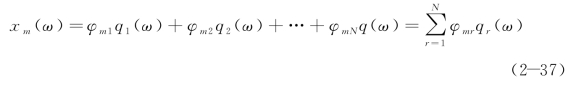
式中 φmr—— 第m 个测点第r 阶模态的振型系数；

qr(ω)—— 第r 阶模态坐标。

由N 个测点的振型系数组成的列向量称为第r 阶模态向量，反映了该阶模态的振动形状。

(https://www.xing528.com)

由各阶模态向量组成的矩阵称为模态矩阵：

由各阶模态坐标组成的向量称为模态坐标：

由式(2-40)与式(2-37)可得系统的响应列向量为

将上式代入式(2-29)中，可得

对于无阻尼自由振动，上式成为

对第r 阶模态，则得

对于阻尼系统，第r 阶模态，有

根据上述理论，利用有限元软件ANSYS对横向稳定杆进行了模态分析。同时根据Craig-Bampton模态综合法，按照低地板城市客车后悬架横向稳定杆的实际铰链施加位置，选择A，B，C，D 四处中心点的节点，将关键点粘贴到这些节点上，并在ANSYS软件中，运行ADAMS宏命令，将模态分析的结果生成到MNF(Model Neutral File)文件中。在ADAMS/View环境下，导入该信息文件，用柔体模型代替相关的部件，并建立与相邻部件的链接关系。由于Craig-Bampton模态综合算法对每个柔性体加了6个非线性刚体坐标，因此横向稳定杆的模态振型有刚体运动，在用多柔体模型进行仿真时，要将这些刚体模态振型屏蔽掉。表2-1显示了横向稳定杆主要的自由振动频率，图2-5至图2-10显示了横向稳定杆的800 Hz以下的自由振动振型图及对应的固有频率。

表2-1 横向稳定杆固有频率计算结果

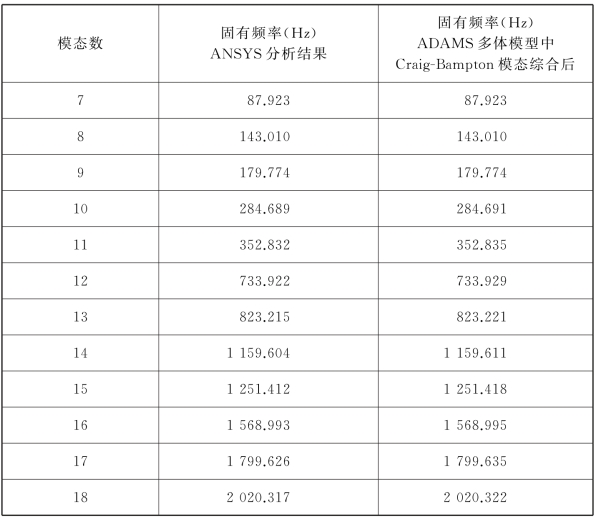
图2-5 模态7，87.923 Hz

图2-6 模态8，143.010 Hz

图2-7 模态9，179.774 Hz

图2-8 模态10，284.691 Hz

图2-9 模态11，352.835 Hz

图2-10 模态12，733.929 Hz