3.5.4.1 火源尺寸
对于火源尺寸,目前还没有明确的规定,可以参考欧洲隧道防火计划(UPTUN)推荐的火源尺寸进行选取,如表3-5所示。
表3-5 欧洲隧道防火计划推荐火源尺寸
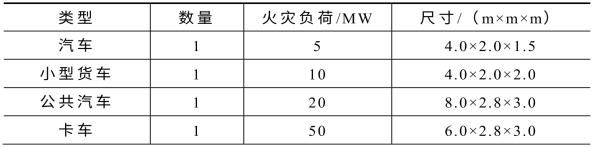
我国《铁路隧道防灾疏散救援工程设计规范》(TB 10020—2017)规定,列车火灾热释放速率可分别取10 MW、15 MW以及20 MW。此时,火源位于着火列车内部,列车截面尺寸为3.3 m× 3.4 m。由于在列车运行模拟时需要设置重叠网格区域,因此需综合欧洲隧道防火计划(UPTUN)推荐值并做适当调整,这里将火源尺寸设定为8 m×2 m×2 m。
考虑到列车的运动,数值计算需要设置有3个计算域,分别是隧道、列车、火源,其中列车和火源是可运动的,隧道是静止的。另外,STAR-CCM+采用重叠动网格技术实现对列车的运行进行模拟,各区域间有重叠,分别是列车与隧道重叠、火源与隧道重叠、火源与列车重叠,如图3-12所示。
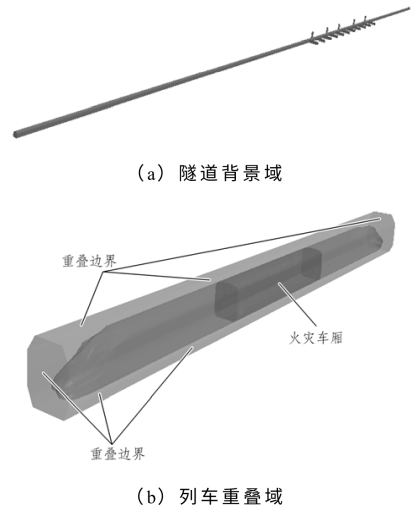
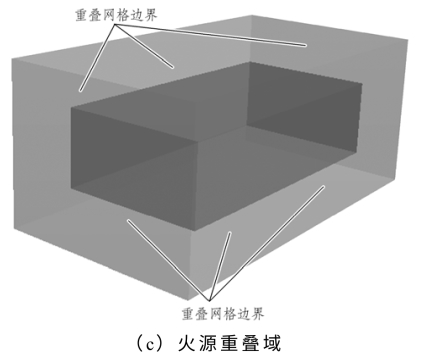
图3-12 计算域划分
3.5.4.2 网格划分
在使用STAR-CCM+进行列车火灾模拟时,需要使用足够小的网格尺寸来反映隧道烟气流动,但软件并没有给出火源网格尺寸的划分原则。可参考火灾动态模拟软件FDS推荐值。FDS火源网格尺寸定义如下:

式中:D*——火源特征直径,m;
Q——火灾热释放速率,kW。
将列车火源热释放速率10 MW、15 MW及20 MW分别带入式(3-24)计算出火源特征直径为2.5 m、2.9 m和3.3 m。而在FDS使用手册中推荐的火源网格尺寸为0.06D*~0.25D*,若取火源网格尺寸为0.2 m,则分别对应于0.08D*、0.07D*、0.06D*,在FDS使用手册中所推荐的火源网格尺寸范围内,因此可以将火车厢内火源网格尺寸为0.2 m。
使用重叠动网格技术对着火列车继续运行时的火灾烟气蔓延特性进行动态计算时,网格类型可以采用多面体网格,火源网格尺寸为设为0.2 m(保证在火源宽度和高度方向有10层网格)。此外,需要对一些特殊结构及区域进行网格加密:
(1)对火源附近进行适当的网格加密,确保火源附近的流场能够反映烟气流动规律。
(2)对列车表面进行加密,可以保持列车表面的形状,以确保列车的气动性能,网格尺寸为0.075 m。
(3)对列车运行区域网格进行加密。最后生成网格如图3-13及图3-14所示。

图3-13 列车体网格生成
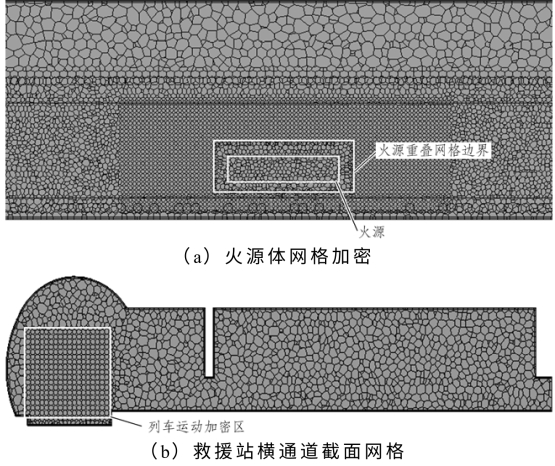
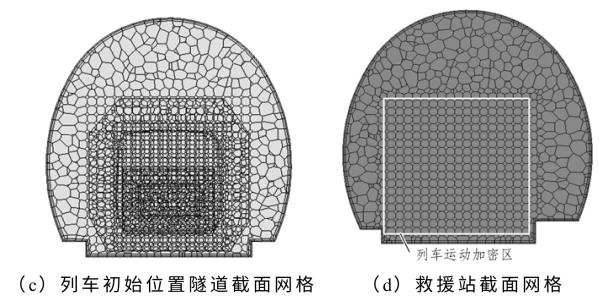
图3-14 隧道各截面网格
3.5.4.3 边界条件
在实际隧道结构中通常含有衬砌结构,衬砌内壁与空气进行对流和辐射换热,而衬砌外壁与土壤接触。由于隧道外土壤覆土层较厚,受外界影响较小,温度近似为恒定值,近似认为衬砌外壁为恒温壁面,可以采取使用等效对流换热系数的方法,建立空气层与土壤之间的联系,即在隧道壁面采用第三类边界条件。而隧道壁面与流体的对流换热系数h,可以首先建立无衬砌的救援站计算模型,设置不同的h值,通过与含衬砌模型隧道顶部纵向温度分布规律计算结果对比,最后得到不同火源热释放速率所对应的h值。火源热释放速率10 MW、15 MW、20 MW时的计算结果如图3-15~图3-17所示。
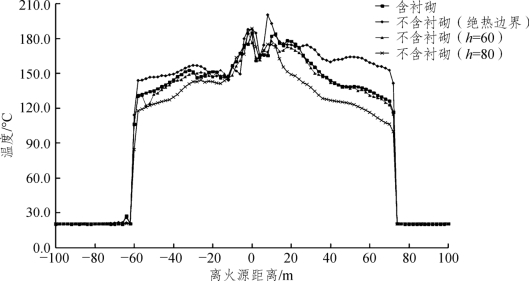
图3-15 源热释放速率为10 MW时救援站顶部温度分布
此外,还需要设置的边界条件有:隧道内初始环境温度、隧道表面发射率、表面粗糙高度、横通道端部防护门的速度入口边界、隧道顶部排烟口的速度出口边界、隧道两端的压力出口边界。
3.5.4.4 隧道活塞风的影响
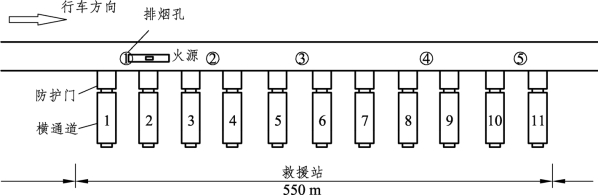
实际运行中,列车运行产生的活塞风对救援站火灾烟气分布是有影响的,因此需要确定活塞风在隧道内对烟气影响的距离。列车在隧道内着火后首先以80 km/h的速度匀速运行,至距离停靠位置时开始制动减速运行,制动停车时加速度为-1.2 m/s2。针对平安隧道,为了分析不同位置火灾的烟气特性,对列车三种停靠位置的烟气特性进行了研究,如图3-18~图3-20所示,其中着火列车停靠在位置1时火源正对着2号横通道,停靠在位置2时火源位于3号排烟口正下方,停靠在位置3时火源正对着7号横通道,且处于3、4号排烟竖井正中间。
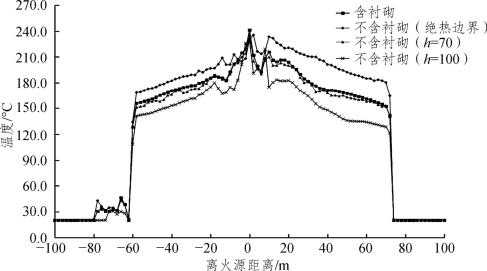
图3-16 源热释放速率为15 MW时救援站顶部温度分布
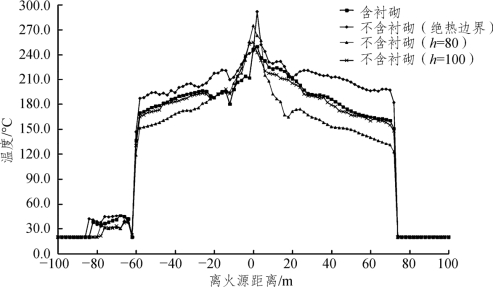
图3-17 源热释放速率为20 MW时救援站顶部温度分布
 (https://www.xing528.com)
(https://www.xing528.com)
图3-18 车停靠位置1示意图
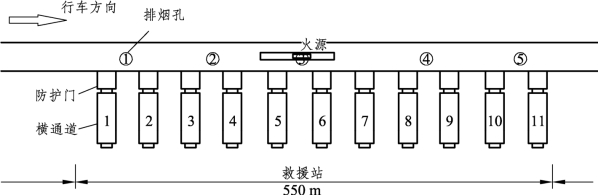
图3-19 车停靠位置2示意图
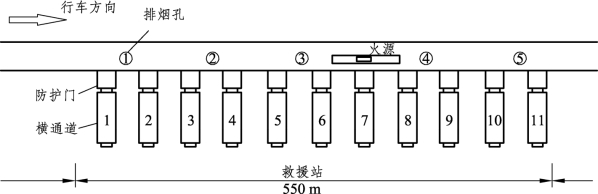
图3-20 车停靠位置3示意图
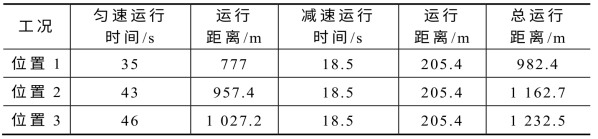
着火列车三种位置工况下的运行时间如表3-6所示。
表3-6 列车运行时间表
着火列车在隧道内继续运行至救援站停车救援时,若考虑隧道内活塞风惯性作用对火灾烟气、温度分布的影响,则需要准确模拟出列车运行所产生的活塞风。由于模型隧道长度有限,不可能与实际隧道的阻力一致,模拟中可以通过在模型隧道两端设置多孔挡板来增加阻力,确保模拟的活塞风与实际隧道中列车运行所产生的活塞风相等,多孔挡板阻力计算如下:
![]()
式中:α——惯性阻力系数;
β——黏性阻力系数。
活塞风模拟计算时通过改变α的大小(忽略β,即β=0)来调整隧道阻力,并可结合一维计算软件SES、活塞风经验公式[25],最后计算出α的值。活塞风经验公式如式(3-26)~(3-29)所示。对于平安隧道,计算结果如表3-7所示,对比SES和公式计算结果,最后确定α的值为15。
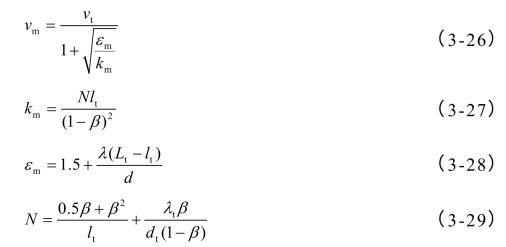
式中:vt——列车运行速度,m/s;
vm——活塞风速,m/s;
km——活塞作用系数;
N——活塞作用常数;
εm——活塞风阻力系数;
β——阻塞比;
Lt——隧道长度,m;
lt——列车长度,m;
λ——隧道与空气间的摩擦阻力系数;
λt——列车与空气间的摩擦阻力系数;
d——隧道断面当量直径,m;
dt——列车断面当量直径,m。
表3-7 活塞风计算结果(m/s)
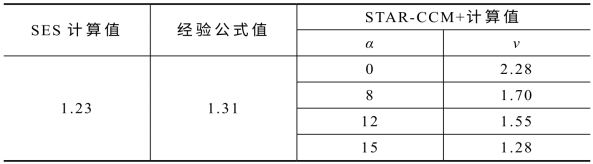
列车以80 km/h的速度运行,列车活塞风模拟结果如图3-21所示,图3-22所示为列车停靠位置1工况下的活塞风变化曲线。
从图3-21分析可知,当列车以80 km/h的速度匀速运行28 s后,隧道内活塞风趋于稳定,此时列车运行距离为622 m,而列车初始位置距离救援站进站端868 m,列车制动减速运行距离为205.4 m,此时有(622+205.4)<868,说明救援站前端隧道长度取1 000 m时满足计算要求。
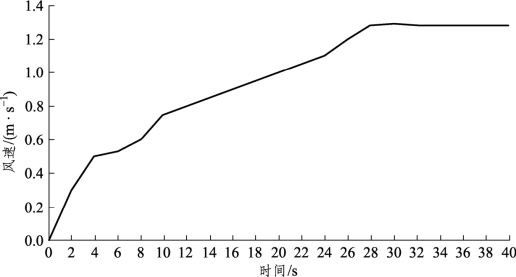
图3-21 以80 km/h运行时活塞风变化曲线
图3-22中列车运行35 s后开始制动减速运行。减速运行初期,由于列车周围环形空间气流向列车运行方向流动,使得隧道内活塞风速略有增加,然后随着列车继续减速运行,活塞风慢慢衰减。
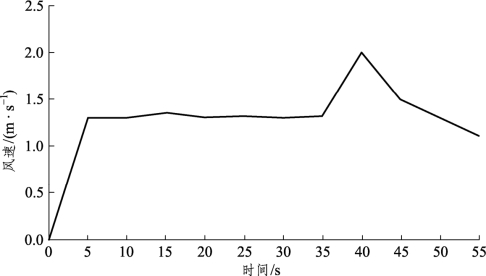
图3-22 车停靠位置1工况下的活塞风变化曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




