在没有受到隧道坡度、列车阻塞以及列车风的影响下，区间隧道火灾羽流未撞击隧道壁面之前的发展特征与自由空间羽流的发展特征相似，自然通风隧道的火灾羽流按照自然空间羽流考虑，Heskestad[63]对自然空间羽流建立如下假设：
（1）火源假定为弱羽流。
（2）火源断面为圆形或者矩形。
（3）羽流在不同高度处的温度和速度分布具有相似性。
（4）羽流各断面处的温度和速度分布为“顶帽型”。
空间的羽流发展特征如图2-2所示。根据上述假设，Heskestad对其建立了质量、动量、能量守恒方程，得到自然空间羽流半径、质量流量和中心速度的数学表达式：
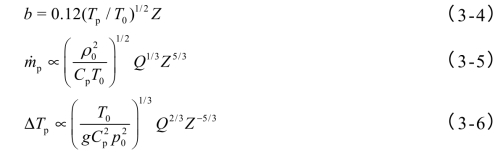
式中：b——羽流半径，m；
Tp——火羽流温度，°C；
T0——周围环境温度，°C；
Z——羽流高度，m；
mp——火羽流质量流量；kg/s；
Cp——比定压热容，kJ/（kg·K）；
Q——火源热释放速率，kW；(www.xing528.com)
g——重力加速度，m/s2；
ρ——气体密度，kg/m3。
火灾烟气在沿隧道的传播过程中，由于与隧道环境的热交换，温度会逐渐衰减，许多学者对此做了相关研究。Delichatsios[64]最早通过研究确定烟气在建筑顶棚下两个相邻挡烟垂壁间的传播机理，给出了火灾烟气沿隧道长度方向的分布；中国科学技术大学胡隆华[13]做了多组全尺寸隧道火灾试验，更好地验证和丰富了前人的相关理论，通过理论推导得到关系式。其中K1=1，K2中的换热系数包含对流换热系数和辐射换热系数两部分，利用平板层流中
的关系式，得到K2的表达式如式（3-7）和式（3-8）所示，所得关系式的预测结果与隧道火灾试验结果吻合度很高。
对于矩形截面隧道：
对于半圆顶截面隧道：
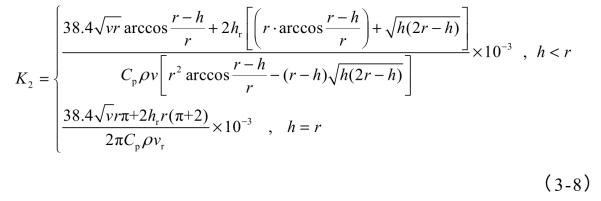
式中：v——火灾烟气沿隧道方向上的流速，m/s；
W——隧道宽度，m；
h——一维烟羽流区烟气层厚度，m；
hr——辐射传热系数，W/（m2· °C）；
r——隧道弧顶半径，m。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
