可移动建筑产品研发设计之活动集割裂算法

运用割裂算法的主要目的是通过按照一定的规则，尽量消减耦合活动集内的信息反馈，并对耦合活动集中的活动进行重新优化排序，形成初始执行次序。这其中的运算规则是保证割裂算法有效性的关键，其主要包括：①识别具有最少信息输入的活动，并将其首先割裂，调整到执行次序的首位。由于该活动对信息输入的需求最弱，所以割裂后它对其他活动产生的影响程度也最小。②当多个活动具有相同的信息输入强度时，具有最大信息输出的活动先执行。③尽量保证被割裂的依赖关系最少，最大程度减小由割裂所造成的信息损失程度。

对耦合活动集运用割裂算法运算的步骤如下（图5－9）。

图5－9　割裂算法运算流程

图片来源：作者绘制

设定：以信息依赖度描述的模糊设计结构矩阵记为TN×N，N为矩阵中活动的数量，Ti为行活动；Seq（Ti）为活动Ti的执行次序，m为正方向执行次序，n为反方向执行次序，m的初始值为1，n的初始值为N；Input（Ti）为Ti的输入信息数量，Output（Ti）为Ti的输出信息数量，Tk为临时活动变量。

步骤一，计算信息依赖度，针对耦合活动集建立以信息依赖度描述的模糊设计结构矩阵T。

步骤二，计算模糊设计结构矩阵T中所有活动Ti输入信息强度Ii，即矩阵各行的信息依赖度值分别相加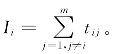，(www.xing528.com)

步骤三，寻找最小输入信息强度Ii的活动Tk（如果存在最小信息强度不唯一的情况，则选择其中具有最多输出信息的活动作为Tk），并转向步骤四。

步骤四，设定Seq（Tk）＝m，从矩阵T中将Tk移除，即T＝T－Tk，并将活动Tk的执行次序向序列前端移动，m＝m＋1，N＝N－1。如果N≠0，则转向步骤五；如果N＝0，则转向步骤八。

步骤五，以割裂次数最少为目标，寻找矩阵T中是否有Input＝0的活动。如果有，则将此活动作为Tk（如果Input＝0的活动数量大于1，则将其中具有最多输出信息的活动作为Tk），并转向步骤四继续运算；如果没有Input＝0的活动，则转向步骤六。

步骤六，以排除非耦合任务为目标，寻找矩阵T中是否有Output＝0的活动。如果有，则将此活动作为Tk（如果Output＝0的活动数量大于1，则将其中具有最多输入信息的活动作为Tk），并转向步骤七；如果没有Output＝0的活动，则转向步骤二。

步骤七，设定Seq（Tk）＝n，从矩阵T中将Tk移除，即T＝T－Tk，并将活动Tk的执行次序向序列尾端移动，即n＝n－1，且N＝N－1。如果N≠0，则转向步骤六；如果N＝0，则转向步骤八。

步骤八，运算结束，完成对耦合活动集中活动的优化排序［9］。