耦合活动依赖度求解成果

通过对二元设计结构矩阵运用划分运算之后，虽然已尽可能形成了设计结构矩阵的下三角形形式，完成了研发活动的初步排序，但研发过程中仍存在一系列的耦合活动集。接下来就要运用割裂算法进一步对耦合活动集内闭合信息环进行阻断，对耦合活动集内的活动进行重新排序，以尽量减少信息的循环次数。运用割裂算法需对耦合活动间的依赖关系与依赖强度展开分析，而明确耦合活动间的信息依赖度则是割裂算法的关键。信息依赖度是耦合活动间依赖关系的最终量化指标，以其为度量依据可对耦合活动集内活动执行顺序进行优化。对信息依赖度的求解是以敏感度与可变度为双度量指标，通过运用数值化的模糊设计结构矩阵方法加以实现。

1.敏感度与可变度概念

耦合活动集中的所有活动都存在信息的输入与输出，当运用割裂算法割断活动间的联系时，需要保证割裂后上游活动输出信息的变化程度以及对下游活动的影响程度尽量最小。这两方面要求由构成信息依赖度的敏感度与可变度双指标来体现。

敏感度是指下游活动对上游活动信息输出变化的反应敏感程度。如果具有高敏感度，上游活动信息输出的微小变化便会导致下游活动的巨大改变；反之，如果敏感度低，上游活动需要发生巨大变化才能实现下游活动的改变。可变度是指上游活动传递给下游活动的信息可能发生变化的程度。具有高可变度说明上游向下传递的信息发生变化的可能性大，反之则说明具有低可变度。

根据敏感度与可变度概念，可对耦合活动集内的活动依赖关系做出进一步的解析。对于耦合活动集中所传递的信息而言，其同时是上、下游活动的输出与输入信息。当作为上游活动的输出信息时，由于上游活动可能同时存在多个输入信息，任意一个输入信息发生改变时，都会对输出信息产生影响，因此该输出信息的可变度等同于上游活动的所有输入信息对输出信息影响程度之和；当所传递信息作为下游活动的输入信息时，由于下游活动同样可能存在多个输出信息，当输入信息发生改变时，会对所有下游活动输出信息产生影响，因此该输入信息的敏感度等同于对下游活动的所有输出信息的影响程度之和（图5－7）。通过以上分析可以得出以下结论：构成敏感度与可变度的基本要素是某活动的单一输入信息的改变对单一输出信息的影响程度。基于此结论，对于敏感度与可变度值的计算，还需再引入信息关联对与关联度的概念［9］。

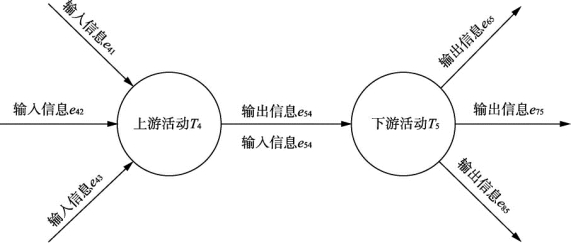
图5－7　活动间信息传递关系示例

图片来源：作者绘制

信息关联对是由上游或下游活动的任意一组输入信息与输出信息所组成的。如图5－7所示，其所包含的信息关联对有（e41，e54）、（e42，e54）、（e43，e54）、（e54，e65）、（e54，e75）、（e54，e85）。关联度是信息关联对中输入信息变化所引起输出信息发生改变程度的度量指标。如果输入信息的细微改变会引起输出信息的巨大变化，那么该信息关联对具有高关联度，反之则具有低关联度。由此我们可以得出：上游活动输出信息的可变度等于上游活动的输入信息与输出信息所组成的所有信息关联对的关联度之和；下游活动输入信息的敏感度等于下游活动的输入信息与输出信息所组成的所有信息关联对的关联度之和。

2.信息依赖度求解的方法与步骤

计算耦合活动集所有信息依赖度的主要步骤为：第一步，首先确认耦合活动集内的所有信息关联对，生成信息关联对集合；第二步，建立模糊一致判断矩阵，对关联对的关联度进行量化，明确关联度值；第三步，通过关联度值计算可变度与敏感度，分别构建可变度矩阵与敏感度矩阵；第四步，整合可变度与敏感度两指标，得到信息依赖度值（图5－8）。

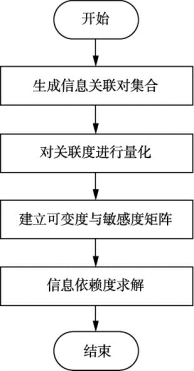
图5－8　信息依赖度求解流程

图片来源：作者绘制

（1）生成信息关联对集合(www.xing528.com)

生成信息关联对的具体操作是：首先针对耦合活动集矩阵内的每一个活动进行有效输入与输出信息的分析与确认；然后将该活动的输入信息与输出信息进行逐一配对，形成单独活动的信息关联对集合；最后将所有单独活动的信息关联对进行组合，形成耦合活动集的信息关联对集合。

（2）对关联度进行量化

信息关联对的关联度是无法直接定量赋值的，其需要凭借实际工作经验与知识积累，以一定的评价标准与规则对其进行主观量化判断。关联度评价的对象是耦合活动集中信息关联对的关联度集合，记为D＝｛d1，d2，…，dm｝。对关联度进行量化具体操作方法是：

首先需要采用0.1至0.9的模糊性评价标度（表5－1），同时对关联度集合中的所有元素进行两两比较，形成任意两个关联度之间相对重要性的定量描述，建立起两两比较判断矩阵，也称为模糊互补矩阵F＝（dij）m×m。其中m表示矩阵所要比较关联度的数量，di表示行关联度，dj表示列关联度，dij则表示第i个关联度与第j个关联度相比较的高低程度。

表5－1　关联度比较标度

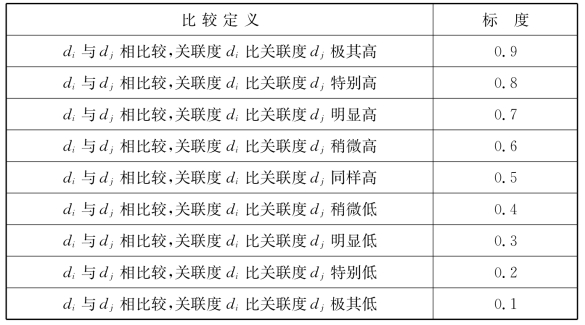
表格来源：范周田.模糊矩阵理论与应用［M］.北京：科学出版社，2006：216

然后，将模糊互补矩阵F转变为模糊一致矩阵R＝（rij）m×m，具体转变运算公式为rij＝（ri－rj）／2m＋0.5。其中ri表示模糊互补矩阵中第i行各评价标度之和，即［10］。

接下来，在已建立的模糊一致矩阵基础上求解关联度值，关联度，而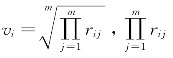为模糊互补矩阵中第i行各评价标度之积［11］。

（3）建立可变度与敏感度矩阵

通过执行此步骤以得到可变度与敏感度数值，为计算信息依赖度值奠定基础。具体操作方法是：首先确认耦合活动集中所有的信息依赖关系；当该依赖信息作为输出信息时，找出所有相关联的上游输入信息与其所构成的信息关联对，将所有信息关联对对应的关联度值进行相加便得到该依赖信息的可变度；同理，当该依赖信息作为输入信息时，找出所有相关联的下游输入信息与其所构成的信息关联对，将所有关联度值进行相加便得到该依赖信息的敏感度；最后，将可变度与敏感度值赋给耦合活动集中的相应依赖信息，建立起可变度矩阵U与敏感度矩阵V。

（4）信息依赖度求解

接下来为了便于运用割裂算法对耦合活动集进行排序与解耦，需要对可变度与敏感度这两个量化指标进行整合，将其转化为综合单一指标的信息依赖度以表征活动间的依赖关系，并进一步以信息依赖度来构建用于描述耦合活动集的模糊设计结构矩阵。信息依赖度值等于可变度值与敏感度值乘积的平方根，即