在划分算法中进行定耦操作的目的是发现耦合活动矩阵中的耦合任务集,尽可能排除耦合活动矩阵中不存在耦合关系的活动,以及尽量缩小耦合活动集的范围。本书中的定耦操作采用了耦合矩阵的幂运算方法。其运算原理是通过耦合矩阵的n次幂运算来搜索出矩阵中的所有信息回路,进而发现所对应的耦合活动集。所谓信息回路是指信息从一个活动被输出后,经过若干次活动间的传递后,又重新作为输入信息回到原活动。具有s个行列活动的耦合矩阵n次幂能够反映经过n次信息传递而形成信息回路的活动间耦合关系。
对耦合矩阵进行幂运算首先需要在普通矩阵幂运算方法基础上进行一定运算规则的调整,具体调整内容是将普通矩阵幂运算中相乘运算改为取最小值“∧”,将加法运算改为取最大值“∨”[7]。那么当对耦合矩阵Cs×s进幂运算得到n次幂矩阵Cn (n≤s),如果矩阵对角线上出现p个非零元素,且p=n,那么该p个非零元素所对应的活动就组成了一个耦合活动集,通过(s-1)次耦合矩阵的幂运算后,所有的耦合活动集将被识别。如图5-5所示,矩阵C为包含五个行列活动的耦合矩阵,下面对其进行定耦操作以识别其中的耦合活动集。首先对矩阵C分别进行2次方、3次方、4次方及5次方运算,得到矩阵C2、C3、C4、C5;然后,在C2矩阵中可发现对角线上的非零元素为C11与C33,则其说明活动C1与C3构成了2次传递耦合活动集;在C3矩阵中对角线上有非零元素C22、C44、C55,说明活动C2、C4、C5构成了3次传递耦合活动集;在C4、C5矩阵对角线上没有发现新的非零元素,则说明耦合活动集识别已完成。接下来需要进行归一操作,将耦合活动集视为一个整体活动,即分别把C1、C3活动与C2、C4、C5各归一为单一整体活动。
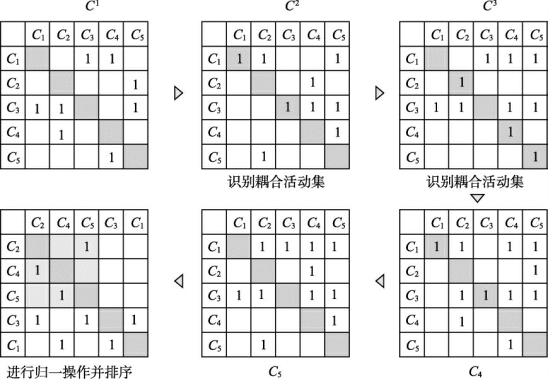
图5-5 耦合活动矩阵定耦操作示例
图片来源:作者绘制(https://www.xing528.com)
然而以上耦合矩阵对角线非零元素p与幂运算次数n相等的情况只是一种理想状态,其一般只适用于研发活动数量较少的简单耦合矩阵。对于研发活动较多的复杂耦合矩阵,真实的情况是:矩阵中可能存在多个具有相同传递次数的信息回路;一个活动可能存在于多个耦合活动集中;或者一个耦合活动集被另一个更大范围的耦合活动集所包含。面对复杂的耦合活动矩阵,在经过幂运算后,矩阵对角线的非零元素p的数量往往会大于幂运算次数n,此种情况下通过幂运算所识别的耦合活动集并非真实的耦合活动集,需要通过对活动间信息传递的回路进行搜索,以再次识别发现真实的耦合活动集。如图5-6所示,其表达了复杂耦合活动矩阵的定耦操作过程。图中根据活动C1、C2、C3、C4、C5相互间依赖关系建立起矩阵C,对矩阵C分别进行2次方、3次方运算,得到C2、C3。矩阵C2的对角线没有两个非零元素,说明矩阵中不存在传递次数为两次的信息回路,即不存在由两个活动组成的耦合活动集。而矩阵C3对角线上存在6个非零元素,则说明由3个活动组成的耦合活动集的数量多于一个,接下来进而需要在这6个活动中搜索信息传递次数为3次的信息回路,最终得到真实的耦合活动集{C1,C5,C3}与{C2,C4,C5}[8]。
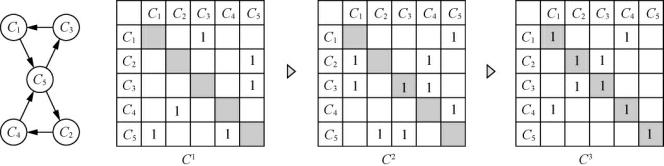
图5-6 复杂耦合活动矩阵定耦操作示例
图片来源:作者绘制
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




