智能汽车设计实践：八皇后算法实现

(1)枚举法

枚举法是最简单的算法,如果单纯地把所有8个棋子摆放的位置全部列举出来,然后对每一种情况作判断,看是否满足八皇后条件,这种处理方法思路当然简单,但是运算量非常大。

加一点约束条件以简化问题。因为要满足八皇后问题的解,每一行、每一列、每一个对角线都只能有一个棋子。所以在摆放第i行棋子时,判断是否可行的方法是考察第i个棋子的控制区域是否和第1到第i-1个棋子的控制区域是否有交叉。即判断第i个棋子和第1到第i-1个棋子是否处于同一列;其次,判断第i个棋子和第1到第i-1个棋子的行数差的绝对值是否等于列数差的绝对值(避免同一对角线)。

(2)回溯法

回溯法有“通用的解题法”之称,它可以提前排除那些不满足条件的状态,比较节省时间。只要当前枚举到的状态有效,就继续枚举下去。当找到一种方案无法继续枚举时,退回到上一个状态,直到达到目标或者所有的可行方案都已经尝试完为止。这就像人走迷宫一样,先选择一个前进方向尝试,一步步试探,在遇到死胡同不能往前的时候退回到上一个拐点,另选一个方向尝试。如图11.54所示的是四皇后回溯的图解。

利用回溯法得到所有八皇后问题的解,一共有92种情况,为了方便后面计算最短路径,将每种情况棋子的位置用棋盘中的序号表示。

八皇后解序列(部分)如下:

图11.54　四皇后回溯示意图

找到所有八皇后的解之后,就需要设计一种行走路径使车模的行程最短,这里设计了两个步骤序列匹配和行程规划来完成这部分工作。

①序列匹配(www.xing528.com)

按照初赛的规则,棋盘中会随机摆放8个棋子,因此这一步要实现的是:找到随机棋子位置与八皇后位置的一一对应关系,使棋子移动到八皇后位置的距离最短。八皇后位置匹配图如图11.55所示,黑色矩形代表随机棋子,红色矩形代表皇后。

图11.55　八皇后位置匹配图

由此设计一个二维距离矩阵如下:

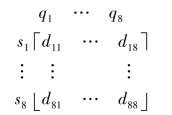
定义si为第i个随机棋子的位置,si=(Row,Colmn),Qj为第j个皇后的位置Qj=(Row,Colmn)。Dij为第i个随机棋子到第j个八皇后位置的距离,距离为两个位置的横坐标和纵坐标差值之和。

应用贪心算法,从这个矩阵中找到最小的值,即一个随机棋子到一个皇后的最短距离,然后删除矩阵中对应棋子的行,删除矩阵中对应皇后的列。这样,会变成7×7的矩阵,然后重复上面的操作,直到矩阵变成空矩阵,这就得到了随机棋子与皇后对应关系的序列。

贪心算法是指在对问题求解时,总是做出在当前看来最好的选择。也就是说,不从整体最优上加以考虑,所做出的是在某种意义上的局部最优解。它是从问题的某一个初始解出发一步一步地进行,根据某个优化规则,每一步都要确保能获得局部最优解。若下一个数据和部分最优解连在一起不再是可行解时,就不把该数据添加到部分解中,直到把所有数据枚举完。

如果要找到全局最优解,那么需要枚举8种情况,时间很长、占用资源多。对于这个棋盘格,最长的距离也不过14个方格,每个匹配之间的距离差距不大,因此局部最优解和全局最优解的差距也不会太大。而且贪心算法只需要8次排序动作,所以这种方法得到最短匹配距离是可行的。

②行程规划

上面的算法已经实现了随机棋子与皇后点的匹配,但从哪个棋子开始摆放,以及每次将棋子搬运到皇后位置之后,选择剩下的哪个棋子作为下一个搬运对象还没有确定。

这里依然采用贪心算法的思路。随机选择一个棋子作为第一个搬运的棋子,将这枚棋子搬运到指定的皇后位置后,计算从当前皇后位置到剩下7个棋子的距离,选取当中距离最短的棋子作为下一个待搬运的棋子,如此反复,直到全部棋子都移动到皇后位置。循环8次,就可以得到每种选择情况下从皇后位置移动到下一棋子的距离。再加上之前已经得到的棋子搬运到皇后的距离,可以得到总移动距离。选出最短的总距离,就能得到匹配序列和行程规划。