完成直立控制有两个前提,一是对姿态传感器读出来的数据进行姿态解算,二是对克服传感器在运行过程中由抖动产生的噪声,这一点通过卡尔曼滤波可以得到相对稳定的信号。当解决这两个问题后,就可以用PD控制来实现对车模的直立控制。
简单来说,卡尔曼滤波器是一个“optimal recursive data processing algorithm(优化自回归数据处理算法)”,它在测量方差已知的情况下能够从一系列存在测量噪声的数据中,估计动态系统的状态。Kalman滤波便于计算机编程实现,并能够对现场采集的数据进行实时的更新和处理,是目前应用最为广泛的滤波方法,在通信、导航、制导与控制等多领域得到了较好的应用。
卡尔曼滤波器常用于融合不同的传感器数据,能够从一系列的不完全及包含噪声的测量中估计动态系统的状态而得到目标的最优估计,并且具有良好的动态性能,因此在惯性导航系统中得到了广泛应用。使用卡尔曼滤波对陀螺仪和加速度计的数据进行融合,可得到精确的姿态倾角。接下来对kalman算法进行详细介绍。
首先要引入一个离散控制过程的系统,该系统可用式(7.3)所示的线性随机微分方程来描述。
![]()
其次,加上系统的测量,如式(7.4)所示。
![]()
上面两个式子中,X(k)是k时刻的系统状态;U(k)是k时刻对系统的控制量;A和B是系统参数;Z(k)是k时刻的测量值;H是测量系统的参数;W(k)和V(k)分别表示过程和测量的噪声,W(k)和V(k)被假设成高斯白噪声,它们的协方差分别是Q,R(假设它们不随系统状态变化而变化)。
下面详细介绍卡尔曼滤波的实现过程:
①假设现在的系统状态为k,根据模型,基于系统的上一状态而预测现在状态。
![]()
式(7.5)中,X(k|k-1)是利用上一状态预测的结果;X(k-1|k-1)是上一状态最优的结果;U(k)为现在状态的控制量,如果没有控制量,它可以为0。
②系统结果已经更新,但是对应于X(k-1|k-1)的协方差还没有更新,用P表示。
![]()
式(7.6)中,P(k|k-1)是X(k|k-1)对应的协方差;A′表示A的转置矩阵;Q是系统过程的协方差。(https://www.xing528.com)
③有了现在状态的预测结果,再收集现在状态的测量值,结合预测值和测量值,可以得到现在状态(k)的最优化估算值X(k|k)。
![]()
式(7.7)中,Kg为卡尔曼增益。
![]()
④目前已经得到了k状态下最优的估算值X(k|k),但是为了让卡尔曼滤波不断地运行下去,还要更新k状态下的X(k|k)的协方差。
![]()
式(7.9)中,I为1的矩阵。当系统进入k+1状态时,P(k|k)就是式(7.5)的P(k-1|k-1),如此一来,算法就可以自回归的运算下去。
上述五个式子便是卡尔曼滤波器的基本公式了,根据这五个公式,可以很容易实现编程。下面是卡尔曼滤波程序。


经卡尔曼滤波后陀螺仪输出的角度数据曲线如图7.9所示,灰色线为处理前的数据,黑色为处理后的数据,从图中可以看出,处理后的曲线噪声降低很多。在得到滤波之后的角度后,便可以对直立车进行直立控制了。
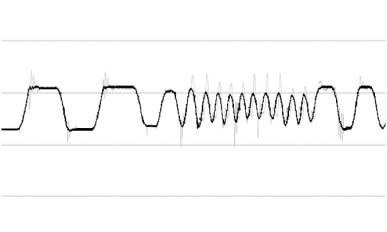
图7.9 卡尔曼滤波前后角度数据曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




