岩溶峰丛洼地水资源分析与开发利用水位消退统计分析

（一）产流判断模型

利用鸳鸯洞2015年9—12月的数据分析水池水位自然消退的速度。

鸳鸯洞内水池水位消退的主要原因是水池底部的渗漏作用。将水池水位的消退视为一个线性过程，即

式中　u——流速；

　　　H——水池的水位；

　　　g——重力加速度。

如果水池出流孔的断面面积为a，则

定义出流孔的排泄系数是Cd，则

列出流量和水位变化的连续性方程：

根据水池的水均衡建立水均衡模型：

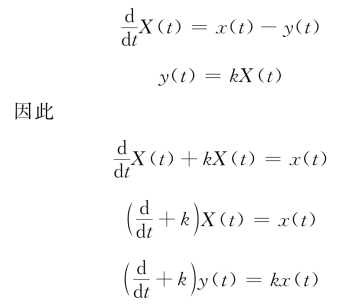
当t=0时，假设水池是空的，在输入函数为δ函数时，例如x=δ（t），表示输入水池的水量为一个体积单位，那么输出函数y（t）=k exp（-kt）时，得

表明水池的排泄速度具有指数衰减的特征。

水池的蓄水量等于指数函数曲线与时间t轴围成图

形的面积，即

水池水位的变化也同样符合指数函数衰减的规律，用公式表示为

选取水池水位衰减的理想阶段分析水位衰减的趋势。水池水位从最高值74cm衰减至30cm，共经历了135天。利用指数函数拟合衰减曲线，得到的衰减方程为

式中　H——水位，cm；

　　　t——时间，天；

　　　k——水池排泄孔的排泄系数，k取0.007；

　　　a——水池的初始水位，即t=0时的水位（见图4-10），这里a取69.628。

图4-10　鸳鸯洞水池水位自然衰减趋势

因为渗漏水池水位一直处于衰减状态，并且其衰减趋势符合指数函数的规律。根据其水位衰减方程，水池水位的衰减速率ΔH与H有关，同样也和衰减时间有关，具有先快后慢的趋势。水池水位的衰减速率ΔH0的计算过程如下：

式中　H0——水池在自然衰减条件下的水位；

　　　a——水池在t=0时的初始水位；

　　　k——衰减系数；

　　　t——衰减时间。

在上式中水位衰减速率ΔH0只与时间有关。对水位衰减方程两边同时进行对数运算，可得

对上式进行变换得到衰减时间t的计算公式：

上式表明时间是与水位对应的，可以根据水位H计算相应的衰减时间t。(www.xing528.com)

根据相邻两天实际水位计算得到的水位变化量ΔH实际上包含了两个变量，其一是水位的自然衰减量ΔH0，其二是因为补给引起的水位增加量ΔH1，即

因此，计算水位增加量，或者在水位变化量中消除水位自然衰减的影响，计算公式为

鸳鸯洞内水池水位的动态受到降雨补给的影响。以2015年为例，在季风气候的影响下，进入6月降雨开始增加，但到了秋季和冬季，降雨减少。鸳鸯洞水池水位增加发生在6月和8月，两个接收补给的阶段都与集中且丰富的降雨对应。而另一方面，水池水位保持稳定的阶段降雨量相对较小，但并非没有降雨（见图4-11）。

水池水位的增长幅度远低于降雨量。2015年6—12月，总计7个月的时间，累计降雨量接近160cm，而水池水位的累计增加量仅为60cm。水池水位的增加量仅仅是同期累计降雨量的37%。水池水位增加量与累计降雨量的比值是局部降雨补给系数R。影响降雨补给系数R的因素包括降雨量的大小和降雨的分配。

图4-11　水池水位的增长量（水池水位增长量与累计降雨量对照）

水池水位的累积增加量与累积降雨量之间近似为对数函数关系，而不是线性关系。一般认为，由于降雨补给满足蓄满产流的机制，水位增量ΔH1与降雨量P的关系可以表示为

上式中，A，B代表系数，当产流面积与降雨面积之间的比例为1时，表示全流域产流，此时A为1；当产流面积小于降雨补给面积时，表示部分产流，A是介于0和1之间的数。B表示地表层对降雨的截流量，B与地表层的初始含水量有关。尽管水位增加量与降雨量之间为线性关系，但是每次降雨A，B的值都有变化，经过多次降雨补给的累积后，水位累积增加量与累积降雨之间变成了近似的对数关系。在降雨充足的条件下，水位累积增加量与累积降雨量之间出现线性关系。但其后降雨补给效率降低，曲线的斜率逐渐减小，即系数A减小，代表产流面积收缩。ΔH—P曲线在中间还出现斜率近似为零的阶段，这表明此阶段降雨量小于截流量，即P＜B，降雨全部被截留，无径流产生。

降雨与水池水位的关系反映了降雨补给的特征。在季风气候条件，降雨补给受到气候特征的影响，出现了两种极端的现象。第一种情况是连续的降雨，降雨补给系数接近1，意味着几乎所有的降雨转化为地下径流，这种情况通常发生在夏季；第二种情况降雨完全被截留，通过蒸散发返回到大气，降雨转化为径流量为0，该情况发生在秋季。降雨入渗的变化通过ΔH—P曲线反映出来。ΔH—P曲线近似符合对数曲线特征（见图4-12）。

在本研究案例中ΔH—P曲线满足的对数函数形式为

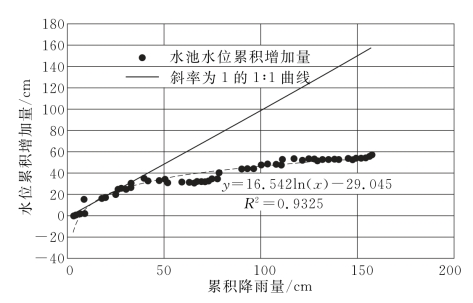
图4-12　鸳鸯洞水池水位累积增加量与累积降雨量的关系

水池水位变化是补给和渗漏共同作用的结果，需要经过运算来区分补给事件发生的条件。在不存在补给的情况下，水池水位的变化反映渗漏的影响，通过水位衰减曲线的拟合分析，证明水池的水位衰减过程满足指数函数的规律。从水池水位变化中扣除水位自然衰减的影响，可以判断补给发生的条件。水池水位的自然衰减速率与水位有关，雨季水位的自然衰减速率高于枯季。扣除水位的自然衰减后，水位的变化速率在零线附近波动，除了一些个别较大的变化速率外，还存在大量的大于零的值（见图4-13），但是并不能用是否大于零来判断补给的发生。

在观测、计算和建模中各种误差导致水位变化ΔH1并不能十分精确地反映补给。为此需要设定一个误差范围。采用箱线图对水位变化ΔH1进行统计。水位变化ΔH1的箱线图如图4-14所示，其中位数为-0.016，非常接近于零，其上下四分位数分别为0.297和-0.200，箱线图4-14选择出14个异常值，将其视为补给发生的标志。

图4-13　水池水位的变化速率（扣除自然衰减的影响）

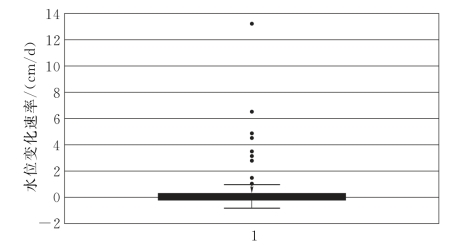
图4-14　水位变化ΔH1的箱线图

由箱线图判断的补给发生时水位的变化反映在水池的水位曲线上，补给发生在水位显著上升的阶段。在没有发生补给的阶段，水位处于自然衰减状态（见图4-15）。

图4-15　水池补给阶段

水池水位的变化量反映降雨补给的多少。根据水池的水位判断是否发生补给，结果显示，降雨补给发生的次数并不多，在2015年6—12月的7个月期间，降雨补给发生了10次。对10次降雨补给进行统计分析，以认识降雨补给的影响因素（见表4-3）。

表4-3　鸳鸯洞水池降雨补给事件统计

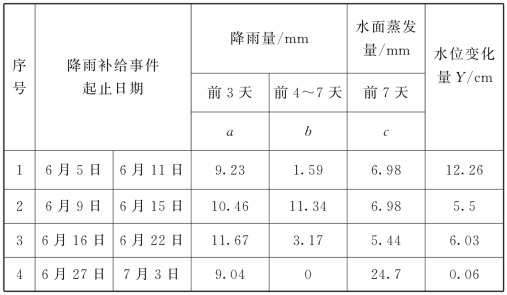
续表

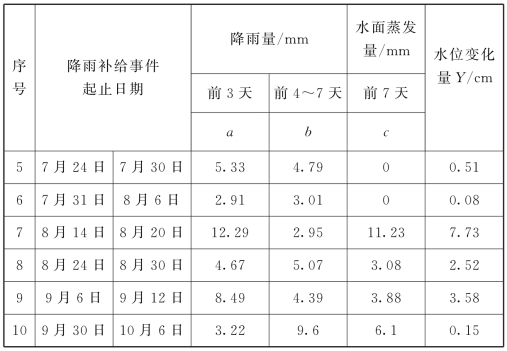
根据饱和产流理论，降雨补给发生的条件与降雨量和地表层的水分含量有关。根据在其他地区的研究结果，选择前3天降雨量，前4～7天降雨量和前7天蒸发量作为因变量。采用线性回归的统计方法建立水位变化量与气候因子的关系。

（二）径流估算模型

以水池水位变化量Y作为因变量，三个自变量a、b、c分别表示降雨补给事件的前3天降雨量、前4～7天降雨量以及前7天累积蒸发量。降雨量数据为凤山县气象站日降雨量数据。蒸发量来自于公式计算结果。采用的公式为Penman水面蒸发量计算公式，采用的数据均来自于凤山县气象站日气象数据。在统计蒸发量时，如当日有降雨则不计蒸发量。

线性回归分析建立的方程为

方程建立了水池补给量与降雨量和蒸发量的关系。这是一个简单的线性关系，表明补给量与降雨量是正相关，补给量与蒸发量为负相关，还存在一个常数。回归分析的相关系数达到90%以上。系数a的置信度达到了99%以上，但b和c的置信度只达到90%以上。

降雨能够形成有效补给需要满足的条件是前一阶段有一定量的降雨，并且降雨量超过一个临界值。在所统计的降雨补给事件中，第四和第六个降雨补给事件仅有少量的补给量，体现了补给发生的临界条件。第四个降雨补给事件虽然前3天降雨量较高，但是前4～7天无降雨，且蒸发量大，所形成的有效降雨也少。第六次降雨补给事件虽然前3天降雨量较少，但是蒸发量极少，也具备了降雨补给的条件。

存在一些极端条件，在这些条件下无法形成有效降雨，或者补给量远大于预测值。例如，利用回归方程预测第一次降雨补给事件的水位变化量为6.89cm，仅相当于观测值的一半。因此第一次降雨补给事件属于一种极端情况。其他没有在统计之列的降雨事件都没有满足降雨补给的条件，它们属于另一种极端情况。对极端条件下降雨补给的预测还需要更多的数据。

（三）讨论

研究区的岩溶石山地区降雨补给是确实发生的。降雨补给与气候关系密切，多雨多补给，少雨少补给。降雨补给是一个“四水”转化的过程，不是结果。这表明降雨补给进行的速度快，因而无法形成有效的蓄水。如果需要从降雨补给的过程获得水资源，需要进行工程调蓄。降雨补给的发生需要满足降雨量条件和初始含水量条件。在这些条件中，近期降雨量最为关键，远期降雨量的影响小。这是因为地表层和包气带的蓄水容量不高，容易在当次降雨事件中得到满足。