地球物理通论：解析地球温度分布

计算地球内部温度分布的方法大致分为两种：一种是借助于热传导方程（可以包含热对流的影响），在获得初始温度、热源分布、热导率等资料的情况下，计算温度的空间和时间分布；另一种是分析地球内部某些与温度有关的现象，例如熔点、相变、相平衡等，由此对实际的温度定出一些界限。把这两种方法结合起来，便得到地球内部温度分布的大体轮廓。

6.4.1 地壳和岩石层的温度分布

在讨论地面热流时，式（6．14）中，q原为地表热流，现将其意义推广到地下深度为Z处的热流（地下热流）。并且，将该式改写为

dT＝－qdZ/K 　（6．16）

取其从地面向下直到Z处进行积分。若地面温度为T0，则

这里的q和K是深度函数。地下热流q与热源分布（即热产率A的分布）有关；地下热导率K与不同深度处的传热机制有关。通常取地表温度T0＝0℃，式中的积分起点为地面，积分终点为深度Z。对于地壳和岩石层，可取K为常数，只讨论q的分布对温度分布的影响。

1）表层

假设地表层内没有热源，则该层内的热流完全由层下热源所提供。此时，表层内和地表热流相等，即q（z）＝q0，将其代入式，可得

T＝q0Z/K 　（6．18）

上式表明，温度将随深度Z而线性增加。这种情况在整个地壳中并不存在，只适用于地下几公里的浅层。对上式两边进行微分，并代入q0和K的数值，q0＝52．3mW/m2， K＝2512mW/（m·℃），不难得出

dT/dZ＝q0/K＝2℃/100m

另外，火山喷发物温度为1000～1200℃，它来自深度为40～100km的火山源，取地表温度为0℃，亦可得出平均温度梯度dT/dZ＝1～3℃/100m。再如，在钻井和矿井中，经过实测，每下降100m，温度提高1～3℃。因此，上述估计值与实测值基本一致。

应该指出，这种情况只适用于浅层几公里的有限范围。在大约5km处，温度为50～150℃（这是唯一可以直接测量的部分）。只是在火山地区，这种温度随深度线性的变化可以向下延伸到几十千米。

2）地壳

假设地壳内有放射性热源，并且富集在上部，由前面知识可知，热产率A随深度Z呈指数衰减，即

A＝A0e－Z/D 　（6．19）

与地表热流公式q0＝q*＋DA0相应，可以写出深度Z处的公式

q＝q*＋DA 　（6．20）

将A的表达式代入上式，则可写出

q＝q*＋DA0e－Z/D 　（6．21）

可得不同深度处的温度分布：

T＝［q*Z＋D2A0（1－e－Z/D）］/K 　（6．22）

式中，q*、D、A0、K均为已知值，从而可以得到温度在地壳内的分布（确切地说，是富集层内的分布）。

3）岩石层

这里的岩石层包括上述的地壳和上地幔部分。波拉克和卡普曼分别就大陆和海洋进行了理论计算。

（1）大陆。采取一维稳态热传导模型，即认为地面热流等于岩石层底部的热流和岩石层内部的热产率之和。热产率A随深度而改变，在不同层次上的数值不同；富集层厚度取8km，地表岩石热产率A0取0．1μW/m3，地壳下部达32km，热产率A1取0．25μW/m3；莫氏面以下为放射性极缺乏的超基性岩层，厚80km，热产率A2取0．01μW/m3，再下面是所谓地幔岩（pyrolite），其热产率A3取0．084μW/m3。热导率取K＝2．5W/（m·K）。作了上述假定后，则可计算不同深度处的温度，如图6．14所示。

（2）海底。采用非稳态的一维热传导模型。其不同时间和不同深度处的温度公式为

T＝T0exp（Z2/4Dt）1/2＋C0Z 　（6．23）

式中，T0为海洋岩石层块体的初始表面温度；C0为其初始温度梯度；D为其热扩散率；Z为其深度；t为其冷却时间。根据式（6．23），亦可算出不同深度处的温度，如图6．14所示。

图6.14 大陆与海底的地温曲线簇

Ⅰ～Ⅲ表示不含水、少量含水、含水的固相线；1～7表示地表热流30、40、50、60、90、120、150mW/m2

图6．14中每一条曲线对应一个地表热流值，依次取30、40、50、60、90、120、150mW/m2，为避免对所得温度曲线任意外推，必须对其变化加以限制，故图中画出不含水、少量含水和含水的三条固相线。从图可以看出，大洋温度曲线普遍高于大陆，如同在150km处，大洋与大陆温差达230K。这样大的温差将造成构造活动的巨大差异，许多与温度有关的上地幔物理性质，如黏滞性、刚度、电导率等将发生巨大变化，从而引起一系列深部作用过程。

在此值得一提的是，可以利用地温曲线与上地幔岩石固相线交点作为上地幔物质开始熔融的深度，即上覆岩石层的厚度，并作出了全球岩石层厚度分布图（图6．15）。该图以12阶球谐函数表示。由图可见，大洋中脊和大陆构造活动区最薄，仅数十千米；而在构造稳定区普遍大于100km；古老地盾区超过300km。

图6.15 由地温曲线和固相线所得全球岩石圈层厚度分布图（单位：km）

在由地热方法所得温度分布曲线基础上构建岩石层厚度分布，是一项突破性的进展，因为在广阔领域上弄清岩石层厚度分布，具有很大理论价值和实际价值。

6.4.2 地幔温度分布

由于对岩石圈层以下的放射性热源分布和热导率知道得很少，因此无法用热传导方程计算地幔温度。而且，处于地幔之中的主要热传输方式，已不是热传导而是热对流，因此，即使采用热传导计算，也会得出不可信的结果。以下简单介绍几种估计地幔温度界限的方法。

1）计算绝热自压温度作为地幔温度的下限

假定地幔没有放射性热源，只是由于自身压力作用使温度升高。这种纯由自压产生的温度，称为绝热自压温度。显然，由于没有考虑内部热源、也没考虑外部的热量输入，完全处于绝热状态，因此所得温度可以作为温度的下限。

按照热力学定律，可得绝热（等熵）情况下的温压变化式：

式中，T为温度；ρ为密度；cp为定压比热容；a为体膨胀系数。由于地球内部偏离力远小于正压力，可视为流体静平衡状态，故

dP＝－gρdr 　（6．25）

式中，r为地球半径；g为重力加速度。将式（6．25）代入式（6．24），并且仅考虑T随r的变化，即将偏微分变为全微分，可得

dT/dr＝－gaT/cp 　（6．26）

根据固体物理理论，式中a/cp在一定假设下可由地震波速度估计出来，即

式中，γ为格林爱森参数（Gruneisen parameter），则得

然后，对式（6．28）的两端积分。积分下限r1对应于岩石圈底部，其温度为T1，则有(www.xing528.com)

这就是计算绝热温度的基本公式。式中积分下限r1对应T1，积分上限r对应T。

在实际计算中，利用地幔中g和γ随深度变化不大的特点，将其从右端积分号中移出。因此，该式中仅有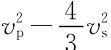随r变化。这个变化己由地震方法得到。若取岩石层的下界（取200km）温度为T200，则可得出地幔最底部，即幔核边界的温度T2900＝1．5T200。当T200＝1500℃时，T2900＝2250℃。这时，整个地幔的平均自压绝热温度梯度为0．28℃/km。所得曲线如图6．16（b）所示。

2）利用电导率随深度变化计算地幔温度

由地磁测深方法可以得到电导率σ（r）的变化。电导率与温度关系极为密切，对于温度的变化极为敏感，因此电导率是用于计算温度变化的有效物理量。

在地幔中，以离子导电为主，属于半导体性质。其离子电导率可表示为

σ＝σ0e－E/KT 　（6．30）

式中，E为激活能，它随压力而变化，可以估计出它在地幔条件下的大小；T为温度；K为玻尔兹曼常数；σ0为常数。总的来看，T随σ的增加而增加。不难写出：

采用班克斯的电导率模型，并取不同的激活能E值，可得到地幔的多条温度变化曲线（图6．16）。用这种办法得到地幔底部的温度为4000～5000K。

图6.16 用电导率σ（z）计算温度T（Z）曲线

（a）电导率随深度变化；（b）温度随深度变化（Ⅰ－Ⅳ表示不同激活能）

3）计算地幔物质熔点作为地幔温度上限

地幔处于固态的岩石层圈之下、液态的外核之上，它是一个多相系统，可能是一种有黏性的处于缓慢对流状态的“软”物质。虽然还不能完全确定它的物理参数，但是它的温度低于物质熔点，是无可非议的。正因为这样，可以用地幔地质熔点作为它的温度上限。估计地幔熔点的方法有两种：

（1）理论计算。熔点理论是固体物理学中进展很慢的一个问题。林德曼提出共振观点：固体原子由于热能发生振动，随温度升高振动加剧，当温度升高到一定程度，造成相邻原子的碰撞从而破坏固体晶格排列时，产生宏观上的熔化现象。这时的熔化温度为熔点，而相应的原子振动频率为临界频率。乌尔芬证明，此临界频率可由地震波速度间接计算出来。由此，可估计幔核边界处的熔点为5300℃。

（2）实验外推。在实验室中可以直接测量在高温高压状态下的岩石熔点。不同压力相应于不同深度，而熔点受压力影响很大，因而可以利用各种岩石的熔点 压力曲线外推不同深度处的熔点。肯尼迪等人于1972年假定地幔物质自上而下可由各种岩石来代表：

橄榄岩200～400km；尖晶石400～700km；方镁石700～900km。

通过实验得到各种物质的熔压曲线，并且将曲线外推到与深度相应的压力区域。这里的压力仍采用流体静压力，故压力仅与深度有关。所得曲线如图6．17所示。在幔核边界处，地幔物质开始熔化的温度为3900K。

图6.17 不同方法所得温度分布综合图

4）由出露地表的地幔岩石性质推断地幔温度

这种方法被比喻为岩石温度计，它属于地球化学或岩石学范畴。基本原理是由于地质作用，有些地幔岩石从深部迁移到地面。在它迁移过程中，因所处的环境条件不同，尤其是温度不同，使得组成不同。通过对这些组成的测定，可以对温度作出估计。

目前利用岩石温度计方法已测到200～300km深度的温度。可以进行这种计算的地幔岩石大致有两种：一种是由于冲顶或断层作用而迁移到地面的大块岩体，如蛇绿岩体；另一种是处于母岩浆中的携带包体（捕虏体），如金伯利岩捕虏体。不同的岩石可测的温度范围不同，例如金伯利岩捕虏体中的透辉石和顽辉石的比例，有效地反映了地下900～1400℃的温度变化。

5）地幔温度总图

上面介绍了4种计算或估计地幔温度的方法。其中第一、第二种，借助于地震学结果（速度分布）和地磁学结果（电导率分布），第三、第四种借助于高温高压实验结果（熔压曲线）和岩石学结果（组成与温度关系）。因此，地幔温度的获得参考了多学科的研究结果。

张少泉将不同方法所得地幔温度分布都放在一张图上（图6．17），并给出一条平均曲线。由图可见顺着深度的坐标，从左到右有这样一些特点：在最顶部，洋区下面的温度变化比陆区大；在软流层内：处于绝热自压线（取γ＝1）与固相线之间，较为单纯，这里具备发生大尺度稳定对流的条件；在地幔底部，温度上升很陡，超过绝热自压线而与液相线重合，在这里为“涌流”或“热点”提供热源；在核幔边界处温度达到3000℃以上。

6.4.3 地核温度分布

研究地核温度的方法，没有研究地幔温度的那么多，最主要的方法是计算绝热自压温度和熔点估计。

1）绝热自压温度

假定外核没有放射性元素，温度分布单纯由绝热自压产生。为此，可沿用绝热自压温度梯度公式（6．26）。

在此，取外核的体膨胀系数a＝3．1×10℃－1，并将相应的g、cp和T的估计值代入，可得

dT/dr＝－0．14℃/km

显然，它比地幔中的绝热自压温度梯度－0．28℃/km低一半。由此得出核幔边界处的温度为3000K。

2）熔点估计

对于熔点的估计与地核的物质组成有关，常分两种情况：

（1）纯铁熔点。假定整个地核由铁组成，外核是液态，内核是固态。那么，内外核的分界处温度，就应该是该压力下的铁的熔点，内核的温度应比熔点低，外核的温度应比熔点高。这是由它们的物态决定的。

金属铁的熔点Tm随压力P的变化为

Tm＝（Tm）0＋a0（dTm/dP）0（1－ρ0/ρ） 　（6．32）

式中，（Tm）0、（dTm/dP）0为零压下的熔点和熔压梯度；a0和ρ0分别为零压下的体膨胀系数和密度。

这里所谈的零压，实际是指常压。将零压下的有关数据代入，则可得到

Tm＝1800＋4560（1－ρ0/ρ）

因为地核内的密度分布已在地震波的速度分布求出，所以代入上式后可直接得出各种深度的熔点。由此得出幔核边界处的温度为4000K，它比由地幔温度计算时得到的相应值高出1000K。

（2）杂质铁熔点。为了实现地幔温度分布与地核温度分布在幔核边界上一致，即避免上述由纯铁计算熔点偏高1000K的不足，促使人们考虑地核可能不是纯铁组成，而是由含有杂质的铁组成。考虑到内核由于密度比铁高，可能含有镍等重金属，从而组成类似铁镍合金的铁内核。

考虑到外核由于密度比铁低，可能含有硫、硅等轻物质，从而组成含有非金属的铁外核。这样，在内外核边界上仍可保持原来铁的熔化温度，而在核幔边界上的温度可以降低1000K，即在3000K左右，从而将地幔温度分布与地核温度分布连为一个整体。

6.4.4 全球温度及热力学参数分布总表

表6．8是斯特西根据全球初步参考速度模型（PREM）导出的全球温度和热力学参数模型。这个全球温度和热力学参数模型与全球速度和力学参数模型是有联系的。导出前者温度分布所需的速度分布资料，就是取自后者。同时要注意到这两个模型的建立过程不同：在速度及力学模型中，基本量是速度分布，而力学量是其派生量；而在温度及热力学模型中，温度并不是直接获得量，相反，往往是先确定热力学参数，再确定温度分布。

表6.8 与PREM对应的温度及热力学参数模型

（续表）