热源分布与传热机制-《地球物理通论》中的研究成果

地表热流的全年总流量达10．26×1020J/a。这是一个十分可观的数字，它超过了那些强烈的地面热现象（如火山喷发、温泉）的全年热流量。这种缓慢却能量巨大的地面热流，其源头在哪里以及是怎样传输到地表的，成为人们关心的问题。

6.3.1 放射性热产率

地球表面的岩石和陨石的放射性元素含量（n）和每种元素的热产率（a）是可以测定的。由此可以计算不同岩石中每种元素的热产率和所有元素的总热产率。

放射性元素的含量很低，通常以1g岩石中含量的10－6g放射性元素为单位，标以10－6g/g或10－6。表6．6给出了几种常见岩石中的放射性含量。通过实验室测定，可知单纯的U、Th、K的热产率分别为

a U＝9．80×10－5mW/g， a Th＝2．63×10－5mW/g， a K＝35．59×10－10mW/g

有了上述数值，则不难算出1g岩石中每种元素的热产率（Ai）和总热产率（A）。现以花岗岩为例，则总热产率为

式中，ni为第i种放射性元素的含量。若要将热产率的单位变成W/m3，则需再乘以花岗岩的密度ρ＝2．65g/cm3，可得A＝3．039μW/m3。

根据上述方法，可以算出每种岩石的热产率，如表6．6所示。应指出，最后一列的数值是单位体积的热产率，如果乘以岩层厚度，则可得各岩层产生的热流密度，这对于估计不同岩层的热流贡献是很方便的。例如，大陆地壳约20km厚的花岗岩层，可产生60．7mW/m2热流；而大洋地壳为5km厚的玄武岩层，它只可产生2．4mW/m2的热流。

表6.6 几种主要岩石的放射性含量和热产率

6.3.2 上地壳的热源分布

对于放射性热源来说，热源的分布就是指热产率的分布。

1）地表热流与地表岩石热产率关系（伯奇关系）

伯奇在1965年首先在美国东部的深成岩地热研究中，发现地表热流与热产率之间存在着线性关系。通常表示成

q0＝q*＋DA0 　（6．5）

式中，q0、A0分别为地表热流和热产率；q*和D称为热流参数。

图6．8给出了澳大利亚前寒武纪地台、英格兰加里东造山带、加拿大地盾和北美的q0-A0数据，它们都落在一条直线上。直线截距相当于q*，直线斜率相当于D。

图6.8 地表热流q0与热产率A0关系

塞斯整理了世界各地的平均q0、q*和D的资料（表6．7）。张少泉在此基础上引入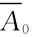值：

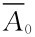的数值可使通过地壳浅部的热产率大小，了解那里的热源情况。

表6.7 大陆地区的热流参数

可以看出地表热流可以分为两部分：一部分是DA0，它来源于地壳浅部的放射性元素富集层，其厚度由D量度，它的变动范围为几千米到十几千米，平均8km，这部分对地表热流贡献约为40％；另一部分是q*，称为剩余热流，包含地壳下部和上地幔的热源影响，约占地表热流的60％。DA0称为浅热源，q*称为深热源。

2）上地壳的放射性热源分布模型

为满足公式所示的热流量和热产率关系，提出三种可能的热源分布模型（图6．9）：

图6.9 上地壳的三种热源分布模型

（a）均匀模型；（b）线性模型；（c）指数模型

（1）均匀模型。假定热产率A在Z≤D范围内为常数，即

A（Z）＝A0，Z≤D

（2）线性模型。假定热产量A在Z≤2D范围内线性减小，即

A（Z）＝A0－Z（A0/2D），Z≤2D

（3）指数模型。假定热产率A在Z≤Z*范围内遵从指数关系减小，即

A（Z）＝A0e－Z/D

式中，Z*为某一深度，在该深度以下的A（Z*）可以忽略不计。

因为放射性热源随深度分布情况无法直接测定，所以上述热源分布模型带有很大猜测性。这些模型只满足热产率沿深度的积分等于该地区的DA0值这个条件。例如，对于均匀模型，Z＝D；对于线性模型，Z′＝2D；对于指数模型，Z′＝Z［要求DA（Z*）＝0］。

这一约束条件，相当于图6．10所示的面积等于DA0。显然，为了从众多的满足面积等于DA0的分布模型中选取合理的模型，还必须考虑其他物理化学条件。

图6.10 大陆地壳的热流和热产率指数模型

岩石学和地球化学研究表明，其中指数模型最接近实际，符合大陆地壳在分异过程中放射性元素的迁移富集规律，被地热学界的广泛采用，成为计算地幔热流、地壳和岩石层内温度分布的重要模型。这一模型不仅适用于上地壳，而且可推广到全地壳（图6．10）。

6.3.3 地幔热流和热源

在确定了地壳内的热源（放射性热产率）之后，则可以从地表总热流中扣除这部分贡献，从而余下来自地幔的热流量。它就是前面所说的剩余热流或深源热流。

1）大陆地幔热流

对于大陆地区，利用地壳热源分布的指数模型，可得出地幔热流计算公式：

qm＝q0－｛（A0－A1）D＋A1［Zm－Dln（A0/A1）］｝ 　（6．7）

式中，Zm为莫氏面深度；A1为地壳下部（放射性元素富集层之下）的岩石热产率；A0为地表岩石的热产率；D为放射性富集层厚度。

从公式可知，为计算全球地幔热流值qm′必须知道q0、A0、D、A1和Zm。其中，Zm可由地震测深得到，通常取Zm＝40km；q0、A0和D可由6．3．2节介绍的方法确定；A1的数值可根据岩石学及地球化学研究结果得知，它相当于麻粒岩热产率（0．2～0．6μW/m3）。因此，从原则上说，并不难确定地幔热流分布。

但是，在实际测定中，由于全球并非所有地区都进行过热流q0的测量和岩石热产率A0的测量，而且放射性元素富集层厚度也难确定，因此常采用如下近似方法：

（1）富集层厚度D的估计。D在不同地区的变化不大，除个别地区如澳大利亚地盾、印度地盾以外，D值大多在8．5±1．5km范围内。D值改变1．5km，对地表热流q0的影响仅8．4mW/m2左右，因此计算时可近似取D＝8．5km。

（2）地表热产率A0的估计。该值在不同的地区是有差别的。然而，要确定A0，必须测定岩石放射性元素U、Th、K的含量。在没有这些测定资料的地区，可以利用剩余热流q*与地表热流q0的经验关系式q*＝0．6q0，可得

将D＝8．5km代入，直接建立A0与q0的关系。

（3）地表热流q0的估计。在做过热流测量地区可以直接取值，在没有实测地区可按照热流值与地质构造和地质年代的关系加以推断（从图6．5直接量取）。

2）大洋地幔热流

对于海洋地区，其热量传输过程不同于大陆，海底随着远离大洋中脊而不断冷却。波拉克和卡普曼利用这样一个非稳态的热过程，求解出如下的海洋地区的地幔热流公式：

式中，K为洋壳热导率；D为洋壳热扩散率；T0为洋壳初始表面温度；C为洋壳初始温度梯度；t为洋壳年龄；Zm为洋壳厚度。

在实际计算中，上列参数取如下数值：K＝3．1W/（m·K），T0＝1200℃，D＝7．5× 10－7m2/（s·K），C＝2．25K/km，Zm＝6．5km。

3）由地幔热流分布看地幔热源

将全球表面分成5°×5°的等积格子，用上述方法算出每个格子的热流值，并做出了以12次球面调和函数表示的全球地幔热流分布（图6．11）。

图6.11 全球地幔热流分布（单位：mW/m2）(www.xing528.com)

将图6．4与图6．11加以比较，可以看出全球的地幔热流与地表热流的分布特征：

（1）全球平均地幔热流为48mW/m2，占全球平均地表热流59mW/m2的80％。

（2）大洋地区的地幔热流平均为57mW/m2，是大陆地区地幔热流平均值28mW/m2的2倍。

（3）大陆地区的地幔热流变化，比起该地区地表热流变化小得多。

（4）大洋地区的地幔热流变化，比起该地区地表热流变化相差不大。

以上几个特点表明，从全球规模上看，地表所观测到的热量，大部分来自地幔，而地壳放射性富集层所提供的热量不足20％。由于大陆地幔热流仅及大洋地幔热流的一半，因此那里的来自地幔的热量就更少了。再考虑大陆内部地幔热流变化小的特点，更加深了这样一个认识：大陆地区的热量来源集中于地壳表层，大洋地区的热量来源集中于地幔。

6.3.4 传热机制之一：传导

固体的经典传热机制是通过自由电子的自由运动和晶格原子的热振动传输热量。这在温度梯度较大的地壳上部是有效的传热机制。但是，温度梯度在几十千米深度以下必然大幅度减小，否则地幔的温度将会超过岩石熔点。因此在温度梯度较小的地球深部，仅靠经典的热传导方式已不能传输足够的热量。那么，那里的热输送采取什么形式呢？

1）热传导（声子传热）

在地面附近的岩石，其热导率可以从实验中测出来的。在常温条件下，岩石通过其晶格原子的热振动传输热能。晶格原子的热运动可以分解出有一定能量并沿温度梯度方向传播的波，一般称为声子（phonon）。

与声子传热机制相应的热导率，表示为Ka，按固体物理理论，它在1000℃下可以写成

式中，ρ为物质密度；vp为平均纵波速度；P为压力；T为温度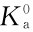；为常数。

显然，这种热导率Ka随压力P的增加而增加、但随温度T的增加而减小，从而造成它随深度的复杂变化。从图6．12可以看出Ka的变化特点：在深度开始增加时，温度增加比较快，压力增加比较慢，总的效果是热导率Ka随深度而减小。到了100～150km（低速层附近），Ka达到极小。过了这个深度，压力的影响超过温度的影响，从而使Ka随深度增加而增加。

图6.12 热导率随深度的变化

2）热辐射（光子传热）

超过100km以后，在一定温度范围内，很多硅酸盐矿物对于红外辐射是“透明的”，即在这种情况下热能如同光线（光子）一样，以辐射形式传播出去。

与光子传热机制相应的热导率，表示为Kb，按固体物理理论，它可以写成

式中，n是折射率；ε是暗度：它在辐射强度的衰减公式（e－εx）中是一个衰减常数，它随频率而异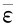，为ε的平均值，对于地球内部可取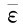＝10cm－1；σ为玻尔兹曼常数。

显然，这种热导率Kb随温度T以三次方形式剧变。例如，对于包含石英和橄榄石的许多矿物，Kb在450℃以上开始增加，在750℃时Kb几乎和Ka相等。可以预计，温度更高时，在地下大约500km以后，Kb将超过Ka，即那里的热辐射作用超过热传导作用。如图6．12所示，在温度为2000℃时，Kb＝0．027，已为Ka的4倍。

3）热激发（激子传热）

在地幔物质中，还可以通过热激发方式，即可以使能量从已激发的原子传递给未激发的原子。热沿着温度梯度方向流动。

与激子传热机制相应的热导率，表示为Kc，按照固体物理理论，它可以写成

式中，E是激发能量（活化能量）；k是玻尔兹曼常数；T是温度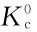；是常数。

显然，激子热导率Kc随温度T的变化取指数形式。激子传热在地球上层的作用是不重要的，它在地幔中要比Ka和Kb作用更大。从图6．12可以清楚地看到，在200～300km以后，Kc已大大超过Ka和Kb。

4）三种传热机制的总和

上述三种机制都以“波”的形式传输热量，它们在不同的深度上对热传输的贡献不同。

一般来说，可以写成总热导率K，即

K＝Ka＋Kb＋Kc 　（6．13）

式中，Ka是声子热导率；Kb是光子热导率；Kc是激子热导率。它们的变化如图6．12所示。如果知道温度梯度d T/d Z和总热导率K，则可计算其热流量q：

q＝－KdT/dZ 　（6．14）

6.3.5 传热机制之二：迁移

上述的传热机制属于“波动”，即物质本身并没有发生迁移。但是，当物质本身处在一定的温度场中，并具有一定流动性时，它可以从高温地点移向低温地点，所携带的热能也随之而迁移。应当说，这是最有效、最直接的传热方式，而且不需要很大的温度梯度。

在地球内部，这种物质迁移是经常发生的。如火山活动、热水活动、岩浆活动、地幔对流（当然，最后一种带有推测性）。可以证明，只要迁移速率达到每年百分之几厘米，物质迁移所传的热，就和上述热传导的量级相当。若速率更高，它将是一种起主导作用的传热方式。

事实上，物质迁移在地幔中可能起一种“热安全阀”的作用：如果地幔中积热太多而又传不出去时，则地幔将变软或部分熔化，以潜热方式积蓄热量，当温度梯度提高和物质黏度降低到一定程度时，将造成热物质流动，同时将热能传到地面。

热对流是物质迁移的一种形式。这种形式在地球内部的物质迁移中，居于重要地位。这里着重加以介绍。

1）瑞利数

如果某层液体接受来自下方的热量，它受热后体积膨胀，周围不受热的液体对它施加一个合成后向上的压力，此压力即浮力F浮，如图6．13（a）所示。F浮等于ρgdV，ρ为密度，dV为由于热膨胀而发生的体积变化。

F浮∝gαβ

式中，g为重力加速度；α为体膨胀系数；β为温度梯度。它们在地球内部的不同深度上是不同的。

图6.13 液体层受力（a）和垂直对流环（b）示意图

同时，由于液体层受到浮力作用，则在上升过程中，必然还会受到来自周围液体施加的与运动方向相反的黏滞力F阻的影响，其黏滞方向向下。

F阻∝μK/ρcp

式中，ρ为密度；cp为定压比热容；K为热导率；μ是运动黏度。

对于一个厚度为h的液体层，当浮力F浮与黏滞力F阻相抗衡时，液体层运动图像发生了变化。为表示这两种力量的抗衡情况，常引用一个无量纲的比值R，其定义为

这个数就称为瑞利数（Rayleigh Number）。

研究表明：当R达到103（临界值）时，就会发生对流。液体出现如图6．13（b）所示对流环。同时，在液面相应地出现六边形格子组成的蜂窝状。其水平尺寸约为液体层厚度的π倍。

2）地核和地幔的瑞利数

对于地球内部能否发生对流，关键在于那里的条件能否使瑞利数达到和超过临界值。

对于地核，可以取g＝5m/s2，α＝5×10－5/K，h＝3000km，ρ＝12g/cm3，cp＝500J/（kg·K），μ＝5×10－7m2/s，K＝3W/（m·K），β＝0．15K/km。将上述数值代入公式，可得

R地核＝1032

显然，该值已远远超过临界值103，因此，地核内肯定可以发生对流。而且对流很强烈，是地核传热的主要形式。这种对流的存在，也为地磁场成因的发电机学说提供了依据。

对于地幔，依照上述办法计算瑞利数。不过，由于上地幔和下地幔的运动黏度不同，能否发生对流，要进行计算才能确定。据估计，上地幔的运动黏度μ＝1025m2/s，所得瑞利数R上地幔可以超过临界值，从而可以发生对流。但是，对于下地幔的运动黏度μ＝1030m2/s，经计算，R下地幔低于临界值，因而不会发生对流。因此，上地幔内的对流是存在的，这又为地球上部岩石圈内发生的板块构造和海底扩张提供有关驱动力源的依据。

应当指出，不同作者从不同角度所得黏滞系数相差很大，因而对于热对流的分布形态的估计也有很大出入。其中，关于是上地幔对流还是全地幔对流还有很大争议。