地球物理通论：电阻率法探测的实质与影响

电阻率法属传导类电法探测。同属传导类电法探测方法的还有充电法、激发极化法和自然电场法等。其中，除自然电场法是一种天然场方法外，其他的方法都是通过人工方法在地下建立稳定或似稳定电流场。

自然界的各类岩石和矿物都具有一定的导电性，但导电性能是有差异的。电阻率法就是通过观测和研究与这些差异有关的天然电场或人工电场的分布规律，达到查明地下地质构造或寻找矿产资源的目的。

4.3.1 电阻率法的理论基础

1）均匀各向同性半空间点电流源的电场

假设电场中的介质是单一的、均匀和各向同性的，地面是一无限宽广的平面，地表以上的空气电阻率趋于无限大，在这种空间建立的电流场称为均匀的、各向同性的半无限空间介质的电场。将两根金属棒A和B相隔一定距离打入地下，当电极距AB非常大时，B电源对所研究的空间范围产生的影响可以忽略不计，B电源认为位于“无穷远处”［图4．13 （a）］，则A电源建立的电场就是一个点电流源的电场［图4．13（b）］。

图4.13 地面点电源的电场

（a）一个点电源装置；（b）地面点电源的电场

假定点电极A进入地下的电流强度为I。在单个点电源的电场中，电流线是以A为中心的辐射线，其方向与电流密度的方向相同。与电流线处处正交的面是电位值处处相等的面，称为等电位面。设地下均匀半无限空间的介质电阻率为ρ，则空间任一观测点M的电流密度值为

式中，r为AM的距离；j为流过截面ΔS的电流强度。根据欧姆定律的微分形式，得到M点的电场强度为E＝j·ρ，于是可求出距点电源A为r处的电位为

由上式可见，以r为半径的半球面上的电位处处相等。

如果电场中两个点电源（图4．14）A和B，大小相等、极性相反，那么地下的电场应是

图4.14 两个异性点电源的电场

A和B各自引起的电场的叠加，也就是两个异性点电源的电场。这样，电场中任一点M的电位UM等于点电源A和B电场在M点电位的代数和，即

2）均匀各向同性介质电阻率的确定

当地面上由A、B点电极向电阻率为ρ的均匀各向同性介质供以电流强度为I的电流时，在地面上任意两点M、N之间产生电位差ΔUMN，A、B称为供电电极，M、N称为测量电极（图4．14）。

按点电源的电场公式可得M、N两点之间的电位差为

式中，K称为装置系数。当各电极位置一定时，K值为常量。

3）视电阻率

在自然条件下，介质（表土、岩层和矿体）大多是各向异性的、不均匀的。按这一方法测得的结果不是某种岩石的真电阻率，而是电流分布范围内，各种岩石电阻率的综合反映，称为“视电阻率”，用符号ρs表示，即

ρs与测量时供电的电流强度I无关，而和地电断面的性质、电极排列有关。视电阻率实质上是在电场有效作用范围内各种地质体电阻率的综合影响值。

在图4．15（a）所示的情况下，除地层ρ1外，地层ρ2对视电阻率ρs的值也有相当大的影响，透镜体的影响很小。在图4．15（b）所示的情况下，地层ρ2的影响减小而透镜体ρ3的影响相当大。因此，不难理解，影响视电阻率的因素有：①电极装置的类型及电极距；②测点位置；③电场有效作用范围内各地质体的电阻率；④各地质体的分布状况，包括它们的形状、大小、厚度、埋深和相互位置等。

图4.15 四极装置建立的电场在地电断面中的分布

（a）ρ3影响小；（b）ρ3影响大

4.3.2 电阻率法的实质

为了揭示视电阻率变化与地下电场分布之间的关系，引入视电阻率的微分表示式。在地表不平、地下岩矿石导电性分布不均匀的条件下，对于测量电极距MN很小的梯度装置来说，MN范围内的电场强度和电流密度均可视为恒定不变的常量。可推导出视电阻率的微分形式：

式中，jMN和ρMN分别表示MN处的电流密度和电阻率；α为MN处地形坡角；j0为地表水平、地下为半无限均匀岩石条件下的电流密度。

如果地面水平，测量电极距MN较小，地下赋存有导电性不均匀体时，上式简化为

图4．16中示出了三种不同的地电断面，若采用同样极距的四极装置，分别于地表测量视电阻率ρs时，将会得到不同的观测结果。图4．16（a）中地下为均匀、各向同性的单一岩石，其电阻率为ρ1。正如前面讨论测定均匀大地电阻率的情况，这时测得的视电阻率ρs就等于岩石的真电阻率值ρ1。图4．16（b）是在电阻率等于ρ1的围岩中赋存一良导电矿体，其电阻率ρ2＜ρ1。良导电矿体的存在改变了均匀岩石中电场分布的状况，电流汇聚于导体的结果使地表测量电极M、N附近岩石中的电流密度jMN比均匀岩石情况下那里的

图4.16 视电阻率与地电断面性质的关系

（a）均匀岩石；（b）围岩中赋存良导矿体；（c）围岩中赋存高阻岩体

正常电流密度j0减小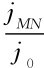，＜1。由于图4．16（b）情况下的ρMN＝ρ，故此时的视电阻率ρs小于均匀围岩的真电阻率ρ1。图4．16（c）是在电阻率等于ρ的围岩中，赋存一局部隆起的高阻基岩，其电阻率ρ3＞ρ1。高阻基岩向地表排挤电流，使测量电极M、N附近岩石中的电流密度比均匀岩石条件下增大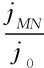， ＞1，ρMN＝ρ1，于是在图4．16（c）条件下地面测得的视电阻率ρs＞ρ1。

4.3.3 电阻率剖面法

电阻率剖面法简称电剖面法。它有多种变种方法，在这些方法中测量电极均沿测线方向逐点进行测量，观测UMN、I，并计算剖面的视电阻率ρs，以探测地下一定深度内地电断面沿水平方向的综合变化。(www.xing528.com)

也就是说不管采用哪一种装置类型，电阻率剖面法在施工作业时都有着相同之处，即用供电电极（A，B）向地下供电，同时用测量电极（M，N）观测电位差，计算视电阻率（ρs），各电极沿测线方向逐点移动、观测。常用装置类型有二极装置、三极装置、联合剖面装置、对称四极装置、偶极 偶极装置、中间梯度装置等。

图4.17 对称四极装置布极示意图

以对称四极装置为例。这种装置的特点是AM＝NB，记录点取在MN的中点上，装置如图4．17所示。其ρs表达式为

电剖面法有较强的适应各种地电条件的能力，它能解决倾角较大（乃至直立）或水平方向电性变化较大的地电断面，如陡倾接触面、构造与基岩显著起伏面、追踪构造破碎带、矿体与溶洞等。电剖面法显示的是地下一定深度（随测点处地下电性环境会有所变化）以上介质的总的导电性能，不能给出测点处地下电性结构，从而也就无法比较相邻测点间地下电性结构的差异。

4.3.4 电阻率测深法探测

电阻率测深法简称电测深法，它是利用不同供电极距来测量某测点视电阻率随深度的变化。常用的装置有三极电测深、偶极电测深、对称四极电测深。这里以对称四极电测深法为例进行介绍，其具体做法是：对于某一个测点，每改变一次供电极距就可测出一个ρs值，从近而远，使电流向地下穿透加深，以此可测得视电阻率随电流穿透深度的关系曲线。在双对数坐标纸上，以AB/2为横坐标，以ρs值为纵坐标，绘制成该测点的电测深曲线。

对称四极电测深法一般用于研究各种近于水平的岩层垂向变化，并定量求出各电性层的厚度及电阻率，了解某些标准层的埋藏深度及起伏情况。

1）水平电测深曲线的类型

电测深曲线的形状是随着地电层的层数、各层的厚度以及各层电阻率值的不同而变化的。

（1）二层电测深曲线。当地层按其电阻率划分为两个电性层时，若上层电阻率为ρ1，厚度为h1；下层电阻率为ρ2，厚度为无限大。两层电阻率之比ρ2/ρ1＝μ2。当ρ2＞ρ1时，称为G型曲线，当ρ2＜ρ1时，称为D型曲线［图4．18（a）］。

图4.18 电测深曲线的类型

（a）二层；（b）三层；（c）四层

（2）三层电测深曲线。三层电性断面有6个参数：ρ1、ρ2、ρ3、h1、h2和h3，其中第三层厚度无限大，根据电阻率ρ1、ρ2、ρ3之间关系大小的变化，三层曲线分为以下4种类型［图4．18（b）］。

H型：ρ1＞ρ2＜ρ3；Q型：ρ1＞ρ2＞ρ3；

A型：ρ1＜ρ2＜ρ3；K型：ρ1＜ρ2＞ρ3。

（3）四层及多层电测深曲线。对于4层电性断面的情况，其电测深曲线的分类可参照三层曲线的分类方法，即先确定上面三层（即第一、二、三层）的曲线类型，再确定下面三层（即第二、三、四层）的曲线类型，然后将这两个已被确定的名称组合在一起，就称为四层断面类型。对4层电性断面而言，可分为8种曲线类型［图4．18（c）］。

HA型：ρ1＞ρ2＜ρ3＜ρ4，HK型：ρ1＞ρ2＜ρ3＞ρ4；

KH型：ρ1＜ρ2＞ρ3＜ρ4，KQ型：ρ1＜ρ2＞ρ3＞ρ4；

QH型：ρ1＞ρ2＞ρ3＜ρ4，QQ型：ρ1＞ρ2＞ρ3＞ρ4；

AA型：ρ1＜ρ2＜ρ3＜ρ4，AK型：ρ1＜ρ2＜ρ3＞ρ4。

每多一层，曲线类型增加一倍，例如5层地电断面的电阻率关系为ρ1＜ρ2＜ρ3＜ρ4＜ρ5的5层电测深曲线，可组合为KHA型，依次类推。

如果电性岩层的层数更多，仍可按上述方法类推。如地层的层数为n，则电测深曲线类型数为N＝2n－1，如5层曲线有16种类型，如“HKH”“HKQ”等。

2）电测深曲线的性质

对于各类测深曲线，无论是二层、三层及至多层的，曲线的首部和尾部均会出现一种渐近线。这种渐近线的特点是：

（1）首部渐近线。由于曲线首部是在供电极距很小时测定的，故电流分布在浅层，其下面各层的电阻率并不影响电流的分布。因而当AB很小时，ρs→ρ1，其渐近线为ρ1。

图4.19 ρ3→∞的三层曲线图

（2）尾部渐近线。当最下层（第n层）的视电阻率不是很大时，由于最下层的厚度为无限大，当AB/2→∞时，可以看成电流主要分布在第n层中，因而可近似地认为ρs→ρn。当ρn→∞时，ρs曲线尾部渐近线为一条与坐标轴成45°角的直线（图4．19）。

（3）等值现象。一组不同的地电断面所测得的电测深曲线形状相同的现象称为等值现象。在三层理论曲线对比中，发现某些参数（μ2＝ρ2/ρ1，ν2＝h2/h1）不同的三层曲线，彼此相差很小（在观测误差5％之内）。进一步研究表明，在相同的A型或H型曲线中，第二层的纵向电导h2/ρ2＝S2或S2/S1＝ν2/μ2是相等的；在K型或Q型曲线中，它们的第二层横向电阻h2×ρ2＝T2或ν2×μ2＝T2/T1是相同的，这种性质称为三层曲线的等值性。如图4．20所示，两个不同的地电断面，由于符合等值原理，故它们的三层曲线完全相同。

图4.20 H型等值曲线

图4.21 等值原理分析图

可用图4．21分析S等值现象的物理实质。对于H（或A）型地电断面，因ρ3＞ρ2，使得第二层中电流的方向近似于与平面平行，电流密度较上、下层大。在第二层内的水平方向导电能力仅由该层的纵向电导S2决定。当断面中的参数ρ1×h1和ρ3不变时，在一定范围内按S2相等的原则改变ρ2和h2的数值，则对电流场分布不会发生明显的影响，观测的ρs曲线也就不变。无疑，中间层厚度h2越小，ρ2与ρ3的差别越大，等值作用的范围也越大。

等值性的存在，使理论曲线数目减少，为定量解释工作带来方便。但同时，它又使对ρ2，h2的解释具有多值性，必须用其他方法求出中间层电阻ρ2之后，才能求得正确的中间层厚度h2。