地球物理通论：磁异常反演与综合推断解释

从前面分析可知，决定磁异常特点的因素主要有4个：磁性地质体的形状和大小，地质体的走向、倾斜及延伸，地质体的磁化强度大小和方向，地质体的埋藏深度。

如果了解了一些有特殊形状磁性体的磁异常特征，就有可能根据地面实际观测的磁异常图像来定量推算磁性体在地下的埋藏情况及其性质。已知磁场的空间分布特征来确定地下所对应的场源体特征，如确定磁性体的赋存空间位置、形状、产状及磁化强度的大小和方向等，这一过程称之为磁异常的反演。

磁异常反演过程分为定性、半定量解释和定量解释两个阶段，这两者是互相关联、互相辅助的。只有通过定性及半定量解释对磁性体形状、产状及其所引起的地质原因进行初步判断后，才能有效地选用定量计算的公式和方法，以便进一步得到更完善的解释结果。在磁异常解释中存在两个普遍的问题。

（1）场源体非均匀磁性问题。在自然界中因场源所处的地质、地球物理环境不同，非均匀磁性是较普遍的现象。通常对具有一定埋深的场源在反演解释中假设其为均匀磁化。

（2）反演的多解性问题，这是地球物理反演解释中普遍存在的问题。为避免或减少磁异常反演的多解性问题，必须充分利用地质及其他地球物理资料进行综合推断解释。

3.7.1 特征点法

利用磁异常曲线上一些特征值，如极大值、半极值、1/4极值、拐点、零值点及极小值等坐标位置和坐标之间的距离，求解磁源体参量的方法称为特征点法。其实质就是求解出不同形状磁性体磁场解析式的特征点与该形体参量间的关系式，然后由异常曲线上读取各个特征值代入相应关系式求得反演结果。

3.7.2 切线法

切线法是利用过异常曲线上一些特征点（如极值点、拐点）的切线之间的交点坐标间的关系来计算磁性体产状要素的方法。这种方法简便、快速、受正常场选择影响小，在航磁ΔT异常的定量解释中得到广泛应用。

1）经验切线法

经验切线法是最早的一种切线法，如图3．17所示。过Za曲线极大值两侧拐点作两条切线，它们与过极值点的切线（若无极小值时，用x坐标轴替代过极小值的切线）有4个交点，其坐标分别为x0、x′0和xm、x′m，则求埋深的经验公式为

h＝0．5×［0．5×（x0－xm）＋0．5×（x′m－x′0）］ 　（3．26）

图3.17 经验切线法

用理论曲线进行实际计算结果表明：经验切线法对顺层磁化无限延伸的板状体（当b＝h时）、垂直磁化有限延伸直立板状体（当b＝h，板长小于埋深时），一般能获得较好的效果。对三度体及其他二度体效果较差。为了提高切线法的计算精度，并能利用多参量求解，人们提出了针对各种形体和斜磁化条件下的带校正系数的切线法。

2）斜磁化二度无限延伸板状体的ΔT异常切线法

由斜磁化二度无限延伸板状体的ΔT异常正演公式，导出极值点的横坐标xmax、xmin，拐点的横坐标x G4、x G1，及特征线段x01、x04、xm1、xm4等14个参数，如图3．18所示。

图3.18 切线法特征线段

图3.19 拐点法参量列线图

为了求得地质体的埋深、宽度和磁化强度，对这14个参数可以有多种组合。合理选择两类组合：一类是以角参量θ为主的组合；另一类是以拐点为主的组合。这些组合均有严格的数学关系式，经计算，编出求磁化强度时的系数列线图（图3．19）或系数表，以便进行切线法反演计算。拐点法计算步骤包括：

（1）由实测ΔT曲线上取的比值。

（2）根据此比值查列线图3．19，确定系数Kh、Kb和Km的值。

（3）按下式求得h、b和Ms：(www.xing528.com)

本方法与正常场选择无关，也不需要确定原点，只要两拐点附近曲线未受干扰即可。这方法在角参量θ≥60°时，均能获得较好的解释效果；且对Za异常求解h和b也适用。

3.7.3 欧拉齐次方程法

欧拉（Euler）齐次方程法又称欧拉反演方法，该方法是一种能自动估算场源位置的位场反演方法。它以欧拉齐次方程为基础，运用位场异常、其空间导数以及各种地质体具有的特定的“构造指数”来确定异常场源的位置。自20世纪80年代中后期以来，欧拉方法已得到较为广泛的应用，尤其是适用于大面积重磁测量数据的解释。

已知一些特殊形状场源的位场为N阶齐次方程，N阶齐次方程也满足欧拉方程，欧拉方程的表达式为

r·ΔT＝－NT 　（3．28）

式中，r为场源点到观测点的距离向量，T是位场异常，N是方程的阶数。该方程的一个解为

T＝k/r N 　（3．29）

在磁异常情况下，k为一常数，N可认为是异常幅值随距离增大的衰减率。针对任意起伏地形，将磁异常视为区域场与点源场之和，当观测面水平时，或尽管观测面不水平，坐标系的两个坐标轴设置成水平并恒定不变，则欧拉方程式可表示为

式中，N为构造指数，B为区域场或背景场。

如果能测量或计算出磁异常及其梯度值，方程中只有5个未知数（x0、y0、z0，B和N）。一般而言，需要根据场源形状或有关异常性质的先验知识来选择构造指数N。这样，可以利用三个或更多相邻观测点的数据（组成一个观测移动数据窗口，对于剖面数据为若干数据点构成的数据段，对于平面网格化数据则通常为矩形数据窗口），通过解方程组计算出场源位置。在整个异常区将移动窗口从一处移到相邻的另一处，可以求得同一场源的多个解，这些解汇聚的位置可以被认为是场源中心点的位置。显然上述公式适用于起伏地形。

理论研究表明，对于一些形状规则的异常源，N为一恒定的正整数。例如，对于单磁极线源N＝1；偶磁极线源N＝2；偶极子源N＝3。对于这些异常源，若能正确地选择N，则利用该方程能够准确地求出异常源的位置。若选择错误的N，将会导致解的发散。

从欧拉方程三维场源参数解的理论分析可知，移动窗口的大小、移动窗口所处位置以及构造指数N值选择的正确与否是影响场源参数数值解稳定性的三个主要因素。

3.7.4 常磁性磁界面迭代反演方法

设界面以下磁化强度恒定，以上无磁性（M＝0），取过平均深度的水平面为起算平面，如图3．20所示。xOy平面的垂直磁化垂直分量磁异常公式为

图3.20 磁界面反演计算

式中，h0为界面平均深度，Δh＝h－h0为界面相对平均深度的起伏。写成近似数值积分形式为

上式为2m×2n个垂直磁化有限延伸直角棱柱体的垂直磁异常之和，即垂直磁化磁性界面垂直磁异常的近似公式。将上式改写为

其中

这是以（k，l）为自由项，以aij（k，l）为系数（平均深度已知），以wij为待求量的线性方程组，由该方程组可解出wij，已知磁化强度M时由wij可计算界面起伏Δhij，而界面深度为hij＝h0＋Δhij。实际计算时常用迭代法，其计算步骤为：①将实际的Za值作为迭代的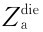值，并给出Δhij的初值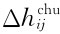；②将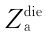（k，l）带入方程组解出迭代中的Δhij的改正值δΔhij，将δΔhij与相加后进行正演计算求Z⊥a的理论值；③计算理论值与实际值的均方误差，当满足：

为止，其中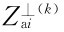为经k次修改界面深度后的界面起伏产生的理论磁异常，ε为实际磁异常的均方误差。如计算的均方误差不小于给定的允许误差，则反复迭代，直到满足迭代精度或迭代次数要求为止。