磁力异常处理和转换：地球物理通论

根据磁异常的数学物理特征，对实测磁异常进行必要的数字处理，使之满足某些特定需要的过程称为磁异常的处理。

磁异常处理的目的有：

（1）使实际异常满足或接近解释理论所要求的假设条件。例如，把分布在曲面上的实测异常换算成分布在同一平面上的异常；把叠加异常分解为孤立异常；或把近似二度异常转换为二度异常等。即把复杂异常处理成简单异常，以便于解释。

（2）使实际异常满足解释方法的要求。例如，由磁场某分量测量结果换算其他分量的值；或者由磁场值转换成为频谱值等。从而可以提供多方面的异常信息来满足一些解释方法本身的要求。

（3）突出磁异常某一方面的特点。例如，通过向上延拓等方法来压制浅部磁性体的异常，相对突出深部磁性体的异常；通过方向滤波或换算方向导数来相对突出某一方向的磁异常特征等。

磁异常的处理和转换主要有异常的圆滑、划分和网格化，解析延拓，分量换算（由实测异常进行ΔT，Za，Ha及Ta之间的分量换算），导数换算（由实测异常计算垂向导数，水平方向导数等），不同磁化方向之间的换算（如化到磁极等）以及曲化平处理（曲面上观测的磁异常转换成在平面上观测的磁异常）等。

磁异常的资料处理包括空间域处理方法和频率域处理方法两大类，随着计算机的广泛应用频率域处理方法具有处理速度快、方法简单等优点而广泛流行起来。

3.6.1 磁异常的圆滑、划分和网格化

1）磁异常的圆滑

类似重力探测，磁异常的圆滑为的是消除测量中的偶然误差和近地表不均匀磁性体产生的干扰，突出主体异常。具体圆滑方法通常采用平均场法，如沿测线的3点、5点或7点圆滑平均，平面的9点、25点圆滑平均等。

2）磁异常的划分

磁异常划分指将叠加在一起的区域异常与局部异常分离开来。插值是常用的处理方法。

3）磁异常数据的网格化

在实际工作中，由于这样或那样的原因，实际测点往往呈不规则分布，但在进行数据处理时，总是要求数据按规则网格分布。需要由不规则网格上的实测异常值换算出规则网格节点上的异常值，这个过程就是数据网格化。显然，数据网格化的问题实际上是插值问题，即用不规则分布的插值节点上的值来计算规则网格节点上的值。

3.6.2 解析延拓

解析延拓是把原观测面上的磁异常通过一定的数学方法换算到高于或低于（但还在场源上方）原观测面的空间处，分别称为向上延拓和向下延拓。

设场源位于z＝H平面以下空间（H＞0），则磁异常场在z＝H平面以上空间是x、y、z的连续函数，具有一阶和二阶连续可微的导数。若z＝0观测平面上的磁异常场T（x， y，0）为已知。由地面磁测数据，计算地面以上空间任意点的磁异常场，在数学上这是解狄利克雷边值问题。根据格林定理和褶积公式，可以得到向上延拓频谱表达式：(www.xing528.com)

式中，ST（u，v，0）为T（x，y，0）的傅里叶变换。

向上延拓处理的主要用途是削弱局部干扰异常，反映深部异常。正演揭示，对于同样大小的地质体，磁力异常随距离衰减的速度与地质体埋深有关。埋深大，磁场衰减慢；埋深小，磁场衰减快。因此，随高度增加，同一剖面上具有磁性但规模小、埋深浅的地质体产生的磁场强度的衰减要比规模大但埋深深的地质体的磁场强度的衰减要快得多。通过向上延拓，增加观测面的高度，可以有效地压制规模小、埋深浅的地质体产生的局部异常，突出深部地质体产生的深部磁异常，由此来研究深部磁性基底结构。

3.6.3 ΔT换算Hax，Hay，Za各分量和化到地磁极

磁测工作中经常性的、大面积的工作只是测定ΔT异常，只在少数场合进行包括Za、Ta、Ha在内的多分量观测，而利用多个分量进行的多参量解释非常有价值，故常需要进行磁异常分量间的转换工作。由磁场与磁位的关系可以得到以下磁场各分量之间的关系式：

式中，t0为地磁场方向单位矢量。

设Sx（u，v，z），Sy（u，v，z），Sz（u，v，z）及ST（u，v，z）分别为Hax（x，y，z）， Hay（x，y，z），Za（x，y，z）以及ΔT（x，y，z）的频谱。利用频谱微分定理可得到上列场各分量导数在频率域内相应的换算关系式：

式中，qt0＝2π［i（l0u＋m0v）＋n0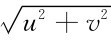］，而（l0，m0，n0）为地磁场方向单位矢量t0的方向余弦。

把ΔT化到地磁极的过程包含了ΔT化Za的分量换算和斜磁化Za化垂直磁化Za⊥的磁化方向换算。前面已经实现了ΔT（x，y，z）与Za（x，y，z）频谱之间的换算，下面来进一步推导斜磁化Za化到垂直磁化Za⊥的公式。

磁化方向换算的方法是由斜磁化的磁场Za求垂直磁化Za⊥方向的磁位U⊥，再由U⊥求Za⊥。

垂直磁化方向的磁位U⊥为

式中，Zal是原斜磁化方向的磁场。上式表明垂直磁化磁位U⊥是Zal沿着原磁化方向tl反方向的曲线积分。

由傅里叶变换可以写出Zal的频谱表达式：

式中，ql是原磁化方向的方向余弦。

因此，由ΔT化到地磁极的转换因子为

若不考虑剩磁，即地磁场方向的方向余弦q0与磁化方向的方向余弦一致，则上式可进一步化简为

由于这种转换相当于把ΔT换算到地磁极的地磁场状态，故称为化到地磁极。