重力异常的正、反演-《地球物理通论》揭示出新成果

重力异常的正演计算，就是给定地下物体形态和密度参数求取在地表产生的重力异常。重力异常的反演计算，就是根据观测的重力异常求取地下异常体形态和密度参数，给出产生此重力异常的剩余密度体在地球内部的分布。

2.6.1 重力异常的正演

分析异常，求取场源，首先必须了解地下不同形状、大小，具有不同密度特点的地质体或地质界面在地表产生的重力异常的特征。在人机交互或选择法对重力异常进行反演时，正演计算也是反演过程的重要组成部分。

1）重力异常正演公式

（1）重力异常的实质。若在大地水准面上的某一点A进行观测，并设地下岩石的密度均匀分布且都为σ0时，其正常的重力为gφ，当A点附近的地下有一个密度为σ的地质体存在，且其体积为V时，这个地质体相对于四周围岩便有一个剩余密度Δσ，其大小为

Δσ＝σ－σ0 　（2．12）

该地质体相对于围岩的剩余质量则为（Δσ·V）。若令它在A点产生的引力为F，则在A点的重力g应为gφ与F之和。由于gφ值达107g．u．的量级，而F值最大仅达103g．u．量级，所以g与gφ两者的方向相差甚微，因而在A点的重力异常为

Δg＝g－gφ＝Fcosθ 　（2．13）

式中，θ为地质体剩余质量所产生的引力F与重力g之间的夹角。

在重力勘探中所称的重力异常，即为地质体的剩余质量所产生的引力在重力方向的分量。若地质体的密度小于四周围岩的密度，则剩余密度为负值，剩余质量也为负值，当然，其重力异常也是负值。

（2）基本公式。以地面上某一点O作为坐标原点，z轴铅垂向下（即沿重力方向），x、y轴在水平面内。若地质体与围岩的密度差（即剩余密度）为σ，地质体内某一体积元dV＝dξdηdζ，其坐标为（ξ，η，ζ），它的剩余质量为dm，则

dm＝σd V＝σdξdηdζ 　（2．14）

令计算点A的坐标为（x，y，z），剩余质量元到A点的距离为R，有

由重力位可知，地质体的剩余质量在A点处对单位质量所产生的引力位为

式中，V为地质体的体积。

因为选择z的方向就是重力的方向，所以重力异常就是剩余质量的引力位沿z方向的导数，即

如果地质体的形状和埋藏深度沿水平方向均无变化，且沿该方向无限延伸，此时的地质体称为二度地质体。将上式中的y轴方向选作二度地质体的延伸方向，积分限由－∞到＋∞，令y＝0，则可得到沿x方向剖面上计算二度体重力异常的基本公式，当剩余密度为均匀时，则可提到积分符号之外，即

式中，S为二度体的横截面积。

同时还可以推导出计算重力异常垂向梯度或重力垂向梯度异常的基本公式和计算重力异常水平梯度或重力水平梯度异常的基本公式及计算重力异常垂向二阶导数或重力垂向二阶导数异常的基本公式。

2）正演计算中模型的简化和组合

在正演计算中，首先是针对一些简单规则几何形状的物体（如球体、水平圆柱体、水平台阶等）计算其产生的重力异常并分析其特征。在实际工作中，某些简单规则地质体，或形状较复杂但距离足够远时，可以近似当作简单规则形体进行研究。如矿巢、矿囊、穹隆构造、某些溶洞可以近似当作球体，扁豆状矿体、两翼较陡的长轴背斜及向斜、大型人工管道等可以当作水平圆柱体来看待。另一方面，复杂地质体引起的重力异常也可以用简单形体异常的叠加得到。如可用一系列微元棱柱体或长方体来构造一个密度界面模型。图2．10所示是一个二度体密度界面的剖面图，计算其产生的重力异常可先将它分解为若干个宽度相同、顶深不同的直立板组合，计算每个直立板产生的异常然后求和就可得到相应界面产生的重力异常。第i个直立板在水平地面（z＝0）x处产生的重力异常为

图2.10 密度界面剖面图

式中，G为万有引力常数；x为观测点水平坐标（m）；x0为柱平面中心点水平坐标（m）；2a为柱水平宽度（m）；D1为柱顶面深度（m）；D2为柱底面深度（m）；σ为柱体密度（剩余密度，kg/m3）。

在地面x处观测到的总异常就是每一个柱体异常的叠加，即

3）简单规则形体产生的重力异常特征

（1）球体（点质量）。对于剩余密度均匀的球体来说，它与将其全部剩余质量集中在球心处的点质量所产生的异常完全一样。将坐标原点选在球心于地面的投影点上。由对称性可知密度均匀的球体产生的重力异常是中心对称的，在平面上，其异常等值线为一簇以球心在地面投影点为圆心的许多不等间距的同心圆，分析其特征只需研究过原点O的任意剖面上异常的分布即可。这里取中心剖面与x轴重合，异常分布的基本特征是：

在x＝0（即原点）处，异常取得极大值。

异常相对原点为对称分布。当z→±∞时，异常值→0。

异常半极值点的横坐标为球心埋深的0．766倍。

水平梯度或方向导数。异常的正负与选择的x轴方向有关，但零值点总是大体对应着球心在地面的投影处，重力异常的垂向一阶和二阶导数，它们在平面上的等值线图会有一圈零值线把正负异常分开，且异常的极值（极大值）所在位置与球心在地面的投影一致。这说明，导数异常阶数越高，异常随深度的增加衰减越快。

因此，在实测重力异常平面图中近于圆形或长短轴差别不大的近椭圆形异常，多半是近于球形地质体产生的。在同一地区，异常越尖锐，范围越小（以x来度量），则该地质体的埋深会越小，反之则会深。

（2）水平圆柱体（水平物质线）。无限长的水平圆柱体在地面引起的异常，完全可以把它当作剩余质量集中在其中轴线的物质线看待。在垂直走向的剖面图上异常特征与球体过中心剖面异常特征类似；但平面图则完全不同，它是一组不等间距的平行直线；中间异常值最大，两边异常值小（实测异常当然不会有无限长的等值线，而是长轴拉得很长的长椭圆形封闭曲线，在长轴线的中间部位就是这种状况）。

（3）铅垂台阶。一些界线清楚的高角度接触带，可等效成铅垂台阶来研究。将坐标原点选在台阶铅垂面与地面的交线上，让z轴与台阶铅垂面垂直，台阶沿z轴正方向和沿y轴均为无限延伸。若以h和H分别表示台阶顶面与底面的深度，在平面等值线图中，是一簇平行台阶走向的直线，数值一边低而另一边高，且在台阶面附近等值线最为密集。只要保持（H－h）不变，不论台阶的上顶埋深如何，Δgmin、Δg（0，0）和Δgmax都不变，只是整条曲线随深度加大而变缓。

2.6.2 重力异常的反演

重力异常的反演就是根据地面上观测的重力异常（场）求出产生重力异常的剩余密度体（源）在地下的分布。

1）反演原则

反演问题是重力勘探，特别是资料处理解释中的主要环节之一，须遵循以下原则。(www.xing528.com)

（1）从观测异常中选择提取适当的用于反演的场值。进行反演必须采用从观测异常中分离出的单纯由反演目标引起的那部分异常值。可以不直接用观测场值而是先将它们作某些变换。例如求出异常的导数和换算至不同高度等，再用变换后的场值作为反演用的原始数据。

（2）选择适当的模型。为了逼近形状不规则的地质体，一般采用一组（多个）而不是单个模型，每个模型的几何形状要尽可能简单。在计算时关键问题是给定模型的初值。并非任意给一组初值，计算机都会计算出接近实际地质体的模型。所以要根据实际的地质、钻井及其他地球物理资料给出接近实际地质体模型参数的初值。

（3）应用合适的计算方法。反演计算过程能否快速、收敛并得到精确的结果，除了给出合适的初始模型外，还取决于所用的计算方法。应针对不同的问题选择合适的计算方法，而且在计算过程的不同阶段要不断调整、修改所用的计算方法。

（4）减少多解性（非唯一性）的影响。与一定的重力异常宽度对应的场源的可能最大深度，就是引起同样宽度异常的点源（球体）的深度。在这个最大深度和地面之间，存在一个可能源的锥形区（图2．11）。同一个异常可以由埋藏很浅的薄透镜体，或不太狭窄的较厚的物体，或球体引起；而且在球体上方较浅的深度上，却由无限多个可能的场源引起这个相同的异常。重力反演中固有的多解性，严重地影响到计算结果的可靠性。采用适当的模型，特别是应用已知资料施加约束，可一定程度减少多解性的影响，并取得比较可靠的结果。

图2.11 引起相同异常的可能源的锥形区

在实际重力资料反演过程中，有直接计算密度异常体几何参数和物性参数的半定量、定量方法，也有针对密度界面的反演。

2）特征点法

特征点法（或任意点法）是根据异常曲线上的一些点或特征点（如极大值点、零值点、拐点）的异常以及相应的坐标求取场源体的几何或物性参数，仅适用于剩余密度为常数的几何形体。

以水平圆柱体模型为例，在垂直走向的剖面图上，根据其产生的Δg异常求圆柱体中心埋藏深度D、线密度λ、半径R及顶部埋藏深度h的公式分别为

这里取Δg异常极值处为x＝0，x1/n为Δg异常极值的1/n处的x坐标值。

3）选择法

选择法的原理是根据实测重力异常在剖面或平面的分布和变化特征，结合工区的地质、其他地球物理和物性等资料，给出引起异常的初始地质体模型，然后进行正演计算。将计算的理论异常与实测异常进行对比，两者偏差较大时，根据掌握的场源体资料对模型进行修改，重算其理论异常。再次进行对比，如此反复进行，以两种异常的偏差达到要求的误差范围时的理论模型来表示实际的地质体。目前在计算机上用得较多的是最优化选择法反演。

设实测异常为Δgk，k＝1，2，…，M，M是用于反演的异常点数；密度异常体模型引起的理论异常用Δg′k表示，它是模型体参数和计算点坐标的函数，即

Δg′k＝f（xk，yk，zk，b1，b2，…，bn） 　（2．22）

式中，xk、yk、zk为计算点坐标；b1，b2，…，bn为模型的n个几何或物性参数。

判定实测与理论异常的符合程度是根据最小二乘原则，即让两者偏差的平方和为最小：

函数Φ称为目标函数。在满足上式的条件下求取模型体的参数。求取模型体参数的过程一般需要下列迭代计算。

（1）给模型体初值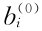，i＝1，2，…，n。0即表示初值。

（2）根据模型体初值计算理论重力异常Δg′k。

（3）根据理论重力异常Δg′k与实测异常Δgk的差别计算模型体参数的修改量δbi，并按下式修改模型：

式中，l为迭代次数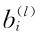；表示本次迭代的初值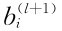；为迭代结果。

（4）判断计算结果是否满足要求。如果不满足，则重复第（2）、（3）步计算。如果满足，本次迭代得到的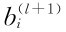就是最后得到的模型参数。

目前应用的最优化方法有阻尼最小二乘法、广义逆矩阵法和共轭梯度法等。

4）频率域密度界面反演

假定Δg（x）表示重力异常，场源层的上部边界为z＝0，下部边界为z＝h（x），这个边界显示界面的起伏。场源层质量位于水平测线之下，这个层在某个有限区D外尖灭。

定义函数h（x）的一维傅里叶变换为

式中，k是变换函数的波数。

根据Parker公式，得到重力异常的一维傅里叶变换公式：

式中，σ为所求地层与下部介质之间的密度差；G为万有引力常量。

从无限和式中提取n＝1的项，并重新排列，得到

假定已知地层与下部介质之间的密度差σ、参考面深度Z0已给定，就可以进行下列迭代计算：

（1）给定界面起伏h（x）的初值，例如h（x）＝0。

（2）将h（x）的初值代人F［h（x）］公式的右端项，计算右端项的傅里叶变换。

（3）对右端项进行傅里叶反变换，即得到一次迭代后的界面起伏h（x）。

（4）判断计算结果是否满足某个收敛标准，或是达到给定的最大迭代次数。如果是，即停止计算；否则转到第（2）步，以本次迭代结果作为初值，继续迭代计算。