地球物理通论：重力异常的高效分离与提取技巧

经校正后得到的重力异常，一方面反映了地下物质密度结构与层状均匀的地球模型之间的不同，另一方面又展示了异常的叠加性，一个测点的重力异常是地下所有具有密度结构异常的地质现象共同产生的。要得到反映地下某种地质现象相关信息（如具有密度差异的沉积盆地基底界面的信息），必须从叠加异常中分离出单纯由这一目标引起的异常，然后进行密度界面反演求出基底界面形态。因此，重力异常的分离是重力资料反演和解释的基础，是重力资料数据处理的主要任务，也是重力勘探工作中最困难的一个环节。

2.5.1 引起重力异常的主要地质因素

引起重力异常的主要地质因素包括从地表到地球深处所有密度分布的不均匀，由深到浅包括地壳深部的因素、结晶基岩内部的密度变化、结晶基底顶面的起伏、沉积岩的构造和成分变化等。

1）地壳深部的因素

根据天然地震及深地震测深资料，地壳结构的模式大体如图2．1所示。在大陆区从地表直到前震旦系结晶基底的顶面，是厚度从零到十几千米的沉积岩层（也有缺失区），密度在2．0～2．7g/cm3；结晶基底以下地壳范围内，是花岗岩类和玄武岩类的物质层，其密度为2．75～3．00g/cm3。花岗岩类与玄武岩类物质层之间也是一个密度分界面，被命名为康拉德（Conrad）面，密度差约为0．2g/cm3。该面在大陆区不能连续追踪。在大洋区，随花岗岩类的消失而消失。在全球范围内可连续追踪的莫霍面，是地壳与地幔的分界面，也是重要的密度界面，通常认为地壳的密度为2．67～2．75g/cm3，上地幔的密度为3．20～3．30g/cm3。

图2.1 地壳结构模式

图2．2为横贯我国东西向、沿北纬30°切取平均布格重力异常和莫霍面深度（地壳厚度的变化）对比图。可见，平均布格异常特征主要对应着莫霍面起伏（即地壳厚度变化）。

图2.2 拉萨—上海平均布格重力异常与莫霍面对比

2）结晶基岩内部的密度变化

结晶基底经历多期次的构造运动及岩浆作用，物质成分和内部构造变得十分复杂，其密度在横向上和纵向上都会有变化。在基底出露区或沉积盖层不太厚的地区，这种密度的变化，会使地表的重力产生相应的变化，其幅度可达数百重力单位。

3）结晶基底顶面的起伏

结晶基底与上覆沉积层通常都存在一定的密度差，在基底内部岩性较均匀的情况下，基岩顶面的起伏能引起较大范围内的重力变化。据此可以圈定出那些范围较大的，具有较大幅度的隆起或凹陷。

4）沉积岩的构造和成分变化

在沉积盆地内部往往存在多个密度分界面，如新生代的疏松沉积物与下伏老地层之间；中新生代的陆相地层与古生代的海相地层之间；古生代上部砂页岩和下部碳酸盐岩之间都可能存在密度差异。当这些界面受地壳运动影响而产生褶皱、断裂，又具备足够大的剩余质量时，会引起明显的重力异常，这为应用重力方法研究、寻找局部构造提供了条件。

此外，沉积层的岩性或岩相变化也可能引起明显的重力变化。例如，在准噶尔盆地山前部位堆积了高密度、体积巨大的砾石，出现了相应的重力高。

5）其他密度不均匀因素

大多数金属矿床（如铁矿、铜矿、锚铁矿等），特别是致密矿石的矿床，其密度都比围岩大，密度差通常超过0．5g/cm3；某些非金属矿（如岩盐、煤炭等）或侵入体，则情况相反，其密度一般比围岩要小。因此，当这些矿体或地质体具有一定的规模和埋藏深度又不大时，可在地表形成测得到的局部重力异常。

地球的所有物质都会引起重力变化。从分量上讲地球的重力场强度主要由地幔及地核中的物质质量所引起，重力场强度平均值的千分之三由地壳物质引起；而且在这么小的重力值中，大约15％才为地壳最上部5km厚的岩石引起。通常研究的地质现象，就存在于这个区域。在这个区域的岩石密度变化引起的重力变化，一般在任何地方都不会超过重力平均值的0．01％。与有经济价值的矿体有关的重力的变化，或许不会超过10－5g。因而，地质构造对于地球重力的贡献非常小。但是因为引力与距离平方成反比关系，对靠近测点的物质密度变化的响应要灵敏得多，依靠高精度的重力观测仪器，可以观测到地壳上部的地质构造现象和有经济价值的矿体产生的重力异常。

2.5.2 区域异常与局部异常

区域异常有时也称背景异常，主要是由分布较广的中、深部地质因素所引起的重力异常。在总场（叠加异常）中，区域异常的特征是具有一定的幅值，影响范围较大，异常具有长波长特点，变化宽缓，水平梯度小。

局部异常主要是指相对区域因素而言影响范围有限的研究对象引起的异常，单个异常分布范围较小，异常具有一定强度但在平面上很快就衰减，异常水平梯度相对较大，具有短波长特点。由于局部异常是从布格异常中去掉区域异常后的剩余部分，故局部异常也称为剩余异常。

图2.3 区域异常与局部异常的相对性

区域异常和局部异常是相对而言的，没有绝对的划分标准，应视研究的问题而言。由图2．3可知，相对异常A而言，异常B和C都可以看成区域异常；而相对C而言，A和B又都可以认为是它的局部异常。

2.5.3 重力异常的分离和提取

划分区域异常与局部异常的方法主要有以下几种。

1）平均场法

平均场法的基本原理是：在一定剖面或平面范围内的区域异常可视为线性变化，因而该范围的重力异常平均值可作为其中心点处的区域异常值；求平均异常时所选用的范围应当大于局部异常的范围。

将布格异常平面图分成正方形网格状，网格大小一般为重力测网点距的数倍至十几倍；然后以每个网格中各节点重力异常平均值作为网格中心点的区域异常值，依据各网格中心点的区域异常值可以勾绘区域异常等值线图，从而各测点上的区域异常便能用内插法求得，相应的局部异常也就可以获得。

另外一种计算办法是采用同一网格的滑动方法求出各节点上的区域异常和局部异常。一般来说，窗口越大，滑动平均值反映的地质体越深。因此，应按需要压制的局部异常范围大小来选择窗口的大小。这种方法最适合于计算机处理，因而应用较广泛。

需要特别指出的是，这类方法应用中必然会带来所谓“虚假异常”的问题，可用剖面上的情况来说明。在图2．4中，用（－L，L）窗口计算A点的局部异常时能够得到正确的区域异常Δgreg；滑动到B点时，因为重力异常平均值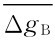大于该点的异常Δg B，所以在B点得到负的剩余异常Δgfau，这是不应有的虚假异常。用人工图解法勾绘区域异常时，就可以避免出现这一问题。处理虚假异常的一种方法是从布格异常中减去第一次求得的剩余异常后，再对其剩余部分重新用（－L，L）窗口求其剩余异常，将第二次求得的剩余异常，再加到原剩余异常中去。如此反复几次，直到基本消除虚假异常为止。

图2.4 产生虚假异常的原因

2）趋势分析法(www.xing528.com)

趋势分析法与滑动窗口平均法是目前重力资料数据处理中常用的方法，参数选择恰当时，可以获得比较理想的分场效果。趋势分析法的原理与异常平滑有相似之处，只不过这里是以一个一定阶次的数学曲面来代表测区内异常变化的趋势，并以此趋势作为区域场来看待，从布格重力异常中减去这一区域异常，即获得测区内的局部异常。

该方法是选用一个m阶（沿测区x，y方向是一样的）多项式来描述全测区的区域异常，m阶多项式的一般形式为

g（x，y）＝α0＋α1x＋α2y＋α3x2＋α4xy＋α5y2＋…＋αM－1ym 　（2．9）

式中，α0，α1，…，αM－1为M个待定系数。若多项式的阶数为m，则M＝0．5（m＋2）（m＋1），g（x，y）即为趋势值（区域异常）。显然，一阶方程代表一个平面，二阶方程代表一个二次曲面，高阶方程则表示了一个高阶曲面。

在做趋势分析时，合适的多项式阶次的选择是取得好效果的关键。多项式阶次的选择，应视区域异常的复杂程度来定，阶次偏高，会造成趋势值受局部异常的影响较大，造成最后的局部异常幅值被削弱。对重力异常的处理来说，一般选用2阶或3阶为宜，复杂地区也只取4阶或5阶；趋势分析法同样也会在分场时出现虚假异常问题，必要时可采用多次迭代的办法予以消除。

3）解析延拓法

根据观测平面或剖面上的重力异常值计算高于（或低于）它的平面或剖面上异常值的过程称为向上（或向下）延拓。

由于重力异常值与场源到测点距离的平方成反比，因此对于深度相差较大的两个场源体来说，进行同一个高（深）度的延拓，它们各自的异常减弱或增大的速度是不同的。进行上延计算时，浅部场源体引起的范围小、比较尖锐的“高频”异常随高度增加的衰减速度比较快；由深部场源体引起的范围大且宽缓的“低频”异常，随高度增加的衰减速度比较慢。因此，向上延拓有利于相对突出深部异常特征。进行下延计算时，由浅部场源体引起的“高频”异常随深度增加（高度减小）的增大速度比较快，而由深部场源体引起的“低频”异常的增大速度比较慢，因此向下延拓相对突出了浅部异常。

解析延拓可以用积分插值法在空间域进行，也可以通过傅里叶变换在频率域进行。

4）高次导数法

依引力公式，其导数的阶次越高，异常随所在测点与场源体距离的加大（或场源体的加深）而衰减越快。在水平方向，基于同样道理，阶次越高的异常范围越小。因此，重力异常的导数可以突出浅而小的地质体的异常特征，压制区域性深部地质因素的重力效应，在一定程度上可以分离不同深度和大小异常源引起的叠加异常。

导数的次数越高，这种分辨能力就越强。图2．5表明，小球的重力异常比大球的小许多，两者的叠加异常很难显示出小球的存在［图2．5（a）］。然而，重力异常的垂向一次导数［图2．5（b）］及二次导数［图2．5（c）］却突出了小球的异常特征，压制了大球的影响。

图2.5 两个不同深度、大小的球体的异常

（a）叠加异常；（b）垂向一次导数；（c）垂向二次导数

图2．6是江苏某铁矿区gzz的异常实例。从Δg平面等值线图［图2．6（a）］上很难发现次级断裂F1，此图只是对F1和F2有些显示，但位置也难确定。F1异常等值线［图2．6（b）］清楚地显示出次级断裂的水平错动；而F2则主要为两侧岩层的相对升降。可见，重力高阶导数gzz具有较好的突出被区域场掩盖、甚至被歪曲了的浅部地质体引起的弱小异常的能力。

图2.6 江苏某铁矿区的Δg（a）和gzz（b）平面示意图

5）用于重力异常数据处理的小波分析

一般深部地质体引起的重力异常特征比较平缓，多是低频成分；浅部地质体引起的异常特征变化比较剧烈，是中高频成分的反映，另外还有采集时受到不同的噪声干扰，也多是高频扰动。早期的重力资料的处理，主要是在空间域进行圆滑、求导以及延拓等处理。傅里叶变换引入后，频率域处理方法得到了广泛的应用，极大地丰富了重力资料处理方法。但傅里叶变换存在对信号局部特征刻画能力不足的缺陷。小波对信号具有自适应性和变焦距的特性，在时频两域都具有表征信号局部特征的能力，利用其特性来对重力异常进行多分辨分析也可实现场的分离。

平面重力异常是二维信号，经过小波分解，得到重力场图像在水平、垂直及对角线方向的高频分量及相应分辨率下的低频分量，由于小波基的正交性，图像小波分解过程中不产生冗余数据。这样，就可以方便地分析信号在不同频带上的频域特性。区域场分离主要利用离散小波变换进行，具体原理为：首先利用高通滤波器G和低通滤波器H对平面重力场沿水平方向进行分解，得到两个子图。然后再对这两个子图平面重力场沿垂直进行小波分解，这样最终得到LL、LH、HL、HH4个子图，LL子图是两个低通滤波器获得的子图（图2．7），它反映了平面重力场的低频成分；类似的，LH主要反映了平面重力场垂直方向上的高频成分；HL反映了平面重力场水平方向上的高频成分；而HH则反映了平面重力场在对角线上的高频成分。如果对低频子图LL进一步分解，又可得到4个子图，如此反复，进行m次小波分解可得到3m＋1个子图。利用小波变换来处理二维重力数据的空间尺度分辨率的分解。经过分解，便可以得到重力数据在不同尺度下的水平、垂直及对角线方向的高频分量及相应分辨率下的低频分量，从而揭示重力数据在不同频带上的特性。图2．8所示为对平面重力数据［图2．8（a）］进行小波分解［图2．8（b）～（e）］和重建［图2．8（f）］结果，图2．8（b）～（e）为小波分解后的低频分量与相应分辨率下的水平、对角线及垂直方向的高频分量，图2．8（f）为小波重构后的重力数据等值线图。

图2.7 二维信号小波分解

图2.8 平面重力数据小波分解和重建

（a）平面重力数据；（b）～（e）小波分解；（f）重建

如图2．9（b）所示，设计的地质体模型中，地质体1与地质体2剩余密度为30kg/m3，埋深为5～15km，模拟上地壳密度不均匀性；地质体3的剩余密度为50kg/m3，埋深为25～50km，表示中地壳密度不均匀；在深度40～66km处为一起伏界面，界面密度差为100kg/m3。由地质体1和地质体2引起的重力异常记为Δg12（x），地质体3引起的异常为Δg3（x），起伏界面引起的异常为Δgu（x），则地面观测异常为它们叠加的异常［图2．9 （a）］，即

Δg（x）＝Δg12（x）＋Δg3（x）＋Δgu（x） 　（2．10）

设Δg（x）＝f（x）∈V0，对它进行小波多尺度分解，有

Δg（x）＝f（x）＝A1f（x）＋D1f（x）＝A2f（x）＋D1f（x）＋D2f（x）　（2．11）

所得结果D1f、D2f和A2f如图2．9（c）所示。

图2.9 二度地质模型及其产生重力异常和小波变换

（a）模型重力异常；（b）地质体模型；（c）Δg（x）小波变换

由图2．9可见，进行了两阶小波分解后，各种尺度成分与地质体之间对应关系比较明显，一阶、二阶小波变换细节D1f与D2f主要反映了上地壳以及上、中地壳介质密度不均匀性，而二阶小波逼近A2f则主要反映深部界面起伏。