理想推进器理论和理想螺旋桨理论是基于推进器在水中工作时水流运动的变化而得到理想推进器和理想螺旋桨的受力表达式，这两种理论有利于对推进器和螺旋桨的水动力产生原因的理解，但是这两种理论都是假定推进器为轴向尺度趋于零且水流可以自由通过的圆盘，完全忽略了螺旋桨的真实形状。理想螺旋桨理论尽管考虑了螺旋桨在旋转过程中会使水流运动加速，然而将螺旋桨假定为无限叶数的虚拟螺旋桨，严重脱离了螺旋桨实际。
螺旋桨的水动力是桨叶几何特殊性和桨叶运动特点巧妙结合而展现出的桨和水的相互作用。本节将结合螺旋桨桨叶几何特征和运动特性来分析桨叶的受力。
螺旋桨桨叶几何特征可以通过叶切面形状及对应的螺距三角形表达，如果将桨叶不同半径处的叶切面形状和对应的螺距三角形作出，并标明其侧斜角与纵倾角值，那么螺旋桨的几何特征就可得到准确表达。螺旋桨桨叶的运动特性可以根据相对运动转换的方式来描述。设螺旋桨的进速为vA、旋转角速度为ω，任取一半径r处的叶切面，如图11-9（a）所示；该叶切面的螺距三角形如图11-9（b）所示。
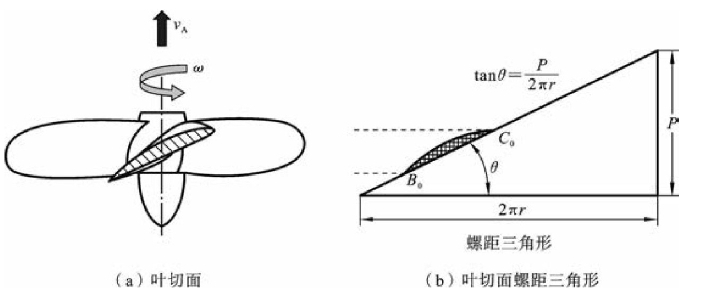
图11-9 螺旋桨叶切面及其螺距三角形
将叶切面随螺旋桨的前进速度转换为远前方来流沿桨轴向的进速vA，将叶切面随螺旋桨的转动速度转换为周围水流相对于叶切面沿桨周向的线速度ωr。螺旋桨的工作会使水流产生轴向诱导速度与周向诱导速度，其中：螺旋桨远后方的轴向诱导速度为ua，周向诱导速度为ut；桨盘面处的轴向诱导速度为ua1=
，周向诱导速度为ut1=
。所以，叶切面周围水流相对于叶切面的运动可描述成如图11-10所示的速度多边形。
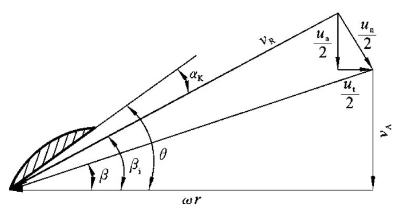
图11-10 速度多边形
根据表达叶切面几何形状特征的螺距三角形，可知叶切面的倾角为θ，即为螺距角，螺距角的表达式为θ=arctan
。根据表达叶切面水流运动情况的速度多边形，在远前方（远前方水的流动未被干扰，轴向诱导速度和周向诱导速度都为零），水流的合速度如图11-10所示，对应的角度β称为进角，进角的表达式为β=arctan
。在叶切面周围的水流由于具有轴向诱导速度ua1=
和周向诱导速度ut1=
，叶切面周围水流的合速度方向相对叶切面的角度为βi，βi称为水动力螺距角，水动力螺距角的表达式为βi=arctan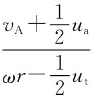
。
当飞机在空中飞行时，前方的空气相当于以一定的速度和角度高速流过机翼，机翼上就会产生巨大的气动升力支撑起飞机的重量（气动升力的方向垂直于来流速度向上），同时也会产生一定的沿来流方向的阻力，如图11-11所示。
与此类似，当水流流过具有机翼剖面形状特征的螺旋桨叶切面时，叶切面上会产生水动力的作用。基于半径r处的叶切面，沿径向取宽度dr得到一个叶元体（叶切面无宽度而叶元体有宽度）。
根据速度多边形，当周围的水流以合速度vR、角度βi流向叶元体时，在叶元体上会产生垂直于合速度vR方向的升力dL和沿合速度方向的阻力dD，设阻力dD与升力dL的比值为ε，ε称为阻升比，则有
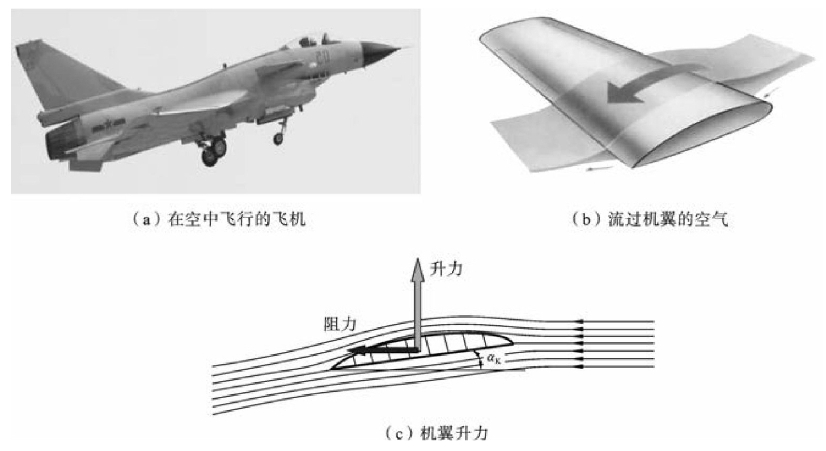
图11-11 飞机、机翼与机翼升力
对螺旋桨关注的是其产生的沿轴向的推力，以及水流对螺旋桨周向的旋转阻力（矩），因此，将叶元体上的升力投影分解到轴向和周向，分别得到轴向上力的分量dLa和周向上力的分量dLt，同时将叶元体上的阻力dD投影分解到轴向和周向，分别得到轴向上力的分量dDa和周向上力的分量dDt，然后再分别合成得到叶元体产生的轴向上的合力dLa-dDa和周向上的合力dLt+dDt，如图11-12所示。
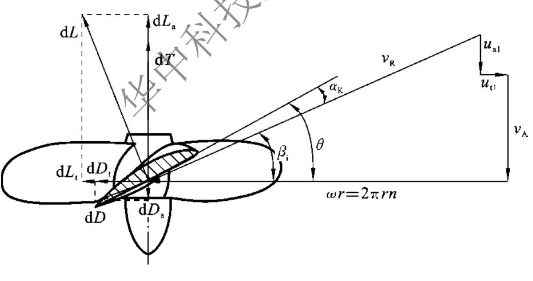
图11-12 螺旋桨叶元体上的受力
很显然，叶元体产生的推力就是
(www.xing528.com)
叶元体旋转时水流对叶元体旋转的阻力矩就是
可见，要使叶元体产生推力dT，外界必须克服叶元体的阻力矩，使其以角速度ω旋转。从功率的角度看叶元体的功能是要产生推力，那么叶元体提供的有效功率为vA·dT；而叶元体有效功率的产生，是以外界克服叶元体相应的旋转阻力矩dQ、带动叶元体以角速度ω旋转为代价的，所以叶元体消耗的功率为ωdQ，那么叶元体效率的表达式为
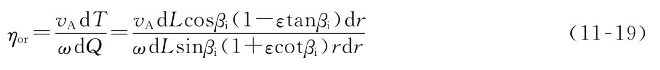
根据图11-12中显示的几何关系可知，
将式（11-20）代入式（11-21）可得：
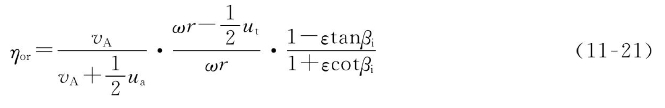
式中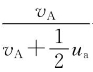 
——轴向诱导效率；
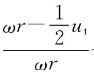——周向诱导效率；
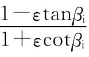——叶元体的结构效率，因为叶元体在有黏性的流体中运动时一定会产生阻力，所以ε一定大于零，即在实际有黏性水流中工作的叶元体的效率一定低于不考虑流体黏性的理想螺旋桨的效率。
对于一个螺旋桨桨叶，其推力和旋转阻力矩可以通过将dT和dQ沿半径方向从叶根至叶梢积分求得，若再乘以对应的螺旋桨叶数，就可得到整个螺旋桨总的推力和转矩：
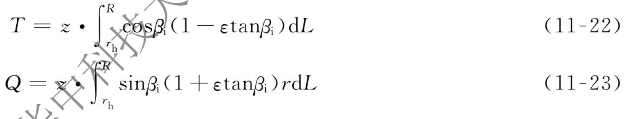
式中 rh——叶根处的半径；
R——叶梢处的半径（即为螺旋桨的半径）。
需要注意的是，式（11-22）和（式11-23）忽略了桨毂的水动力，因为一般情况下桨毂的水动力相对整个螺旋桨的推力和转矩而言是小量，但特殊情况下会有所不同，比如螺旋桨毂帽鳍就是专门通过优化桨毂处的流动来提升整个螺旋桨的水动力性能的，此时桨毂水动力即不可忽略。
螺旋桨在水流中工作时，是在做旋转运动的同时产生推力，由于螺旋桨的旋转运动会受到水流的旋转阻力矩影响，因此外界必须给螺旋桨提供相应大小的转矩。对于整个螺旋桨，设螺旋桨的进速为vA、转速为n，螺旋桨的推力为T、转矩为Q，那么外界（通常是主机）提供给螺旋桨、使螺旋桨旋转的功率为2πnQ，螺旋桨做的有效功率为TvA，可得到螺旋桨的效率为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
