舰艇快速性：理想螺旋桨理论

理想推进器理论表明推进器要产生推力必须要加速水流并使其向后运动。不同的推进器有不同的加速水流的方法，但无法在理想推进器中考虑加速水流的方法。显然，螺旋桨是通过旋转运动推动水流向后加速的，所以螺旋桨在使水流轴向加速的同时还会带动水流周向（旋转方向）加速，如图11-7所示。在动量定理中进一步考虑螺旋桨使水流周向加速的现象，可以得到理想螺旋桨理论的相关表达式。

图11-7　螺旋桨推动水流旋转加速

设螺旋桨的进速为vA，螺旋桨旋转加速水流的旋转角速度为ω。由于在螺旋桨盘面不同的半径处，螺旋桨旋转的线速度不同，因此引起水流的周向诱导速度也不同。为了分析问题的方便，在桨盘面上取一半径为r、宽度为dr的圆环，以此圆环为基础，从圆环处沿流线向上游回溯至远前方，得到远前方水流尚未受螺旋桨影响的位置；从圆环处沿流线向下游延伸至远后方，得到远后方水流受螺旋桨影响结束的位置，得到如图11-8所示的环柱状控制体。

假定在圆环周向上螺旋桨对水流速度的周向和轴向扰动都是均匀的，即将螺旋桨假定为无限叶数的虚拟螺旋桨，不考虑周向位置的不同引起的差异。

根据运动转换，认为螺旋桨不向前运动而是远前方水流以vA的速度大小流向螺旋桨，螺旋桨旋转的角速度为ω。

在远前方，未受干扰的来流轴向速度为vA、周向速度为0；在远后方，受螺旋桨影响结束后的来流轴向速度变为vA+ua、周向速度变为ut；在桨盘面处的水流轴向速度是vA+ua1、周向速度是ut1。

设单位时间内流过环柱状控制体的流体质量为dm，在轴向上运用动量定理，可以得到桨盘面半径r处宽度为dr圆环的推力为

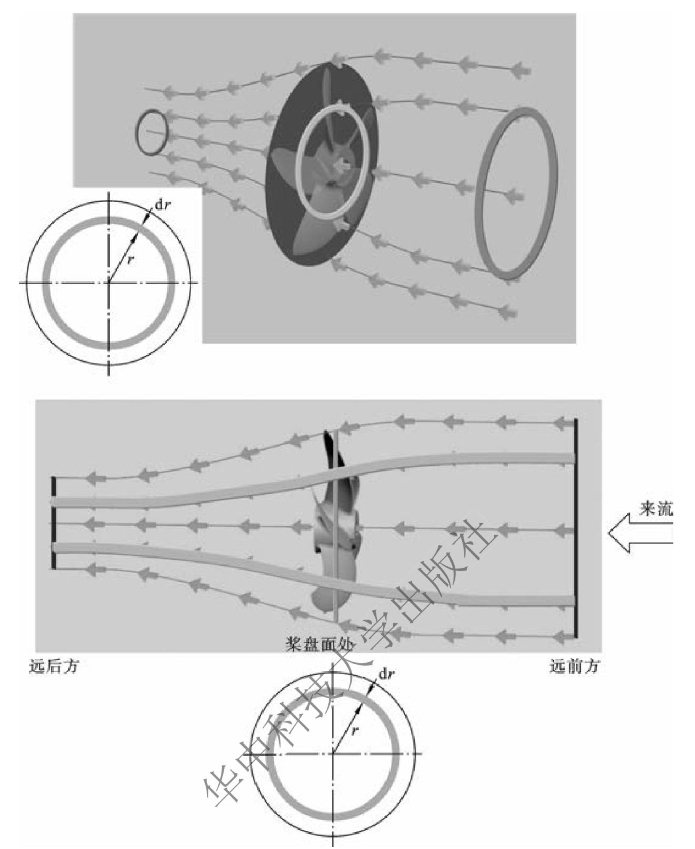
图11-8　理想螺旋桨理论中的控制体

在周向上运用动量定理，可以得到圆环对水流的周向作用力为

根据作用力与反作用力的关系，水流对桨盘面半径r处宽度为dr圆环的旋转阻力就为dm·ut，则旋转阻力矩为dQ=r·dm·ut。即桨盘面半径r处宽度为dr的圆环只有在外界（带动推进器旋转的主机）克服了旋转阻力矩dQ，使其能以角速度ω旋转起来时才能产生dT的推力。

从绝对运动观点看待理想螺旋桨的运动与做功：单位时间内，圆环从外界吸收的功为ωdQ。经过转化后，一部分是推进的有效功，等于推力乘以推进运动的绝对速度，为vAdT；一部分是消耗于水流增加的轴向运动的动能，为·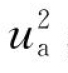；还有一部分是消耗于水流增加的周向旋转运动的动能，为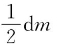·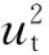。(www.xing528.com)

根据能量守恒，可以建立等式：

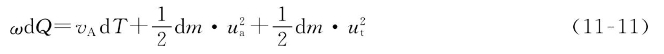
将dQ=rdm·ut、dT=dm·ut代入式（1111）得

该表达式为螺旋桨轴向诱导速度、周向诱导速度、进速和旋转角速度之间的关系。ut和ut1的关系可以根据动能定理推导得到：

单位时间内，理想螺旋桨盘面半径r处宽度为dr的圆环消耗的功为ωrdm·ut，产生的推进有效功为uadmVA，可得到该圆环的理想效率为

将的表达式代入式（11-14）可得

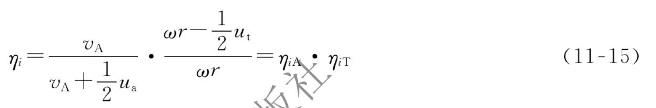
ηiA为理想推进器的效率。由于推进器要产生推力必须使水流加速，获得轴向诱导速度，所以此项必定小于1。此效率也可称为轴向诱导效率。

ηiT称为理想螺旋桨的周向诱导效率。螺旋桨是在旋转运动过程中加速水流使其向后运动并产生轴向诱导速度和推力的，螺旋桨的旋转会导致水流产生周向旋转的诱导速度ut，由于螺旋桨工作时周向诱导速度的存在，所以ηiT=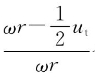也必定小于1。

可见，理想螺旋桨的效率小于理想推进器的效率。