静水面受到扰动就会发生垂向的位移,偏离原静水面,这种静水面的位移在重力和复原力矩的作用下形成往复振荡,这就是可观察的起伏的波面。
这种扰动可以在水面之下产生,也可以在水面之上产生,还可以在水面处产生。
从微观上看,水波是水面及水面下水质点做轨圆运动的综合表现,如图8-20所示。对于同一波面上的水质点P1,P2,…,Pi,其轨圆运动的半径是一样的,并且圆心都是在静水面上。
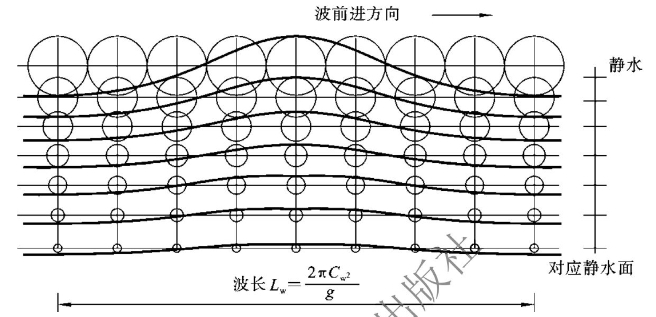
图8-20 水质点的轨圆运动
如图8-21所示,质量为dm的水质点在做轨圆运动时,受到的力分为重力dm·g和离心力dm·ω2r。重力dm·g的大小和方向是不变的;离心力的大小不变,方向取决于水质点在轨圆运动过程中的相位,P1至P5均匀地相差π/4相位角。假设水质点不能受切向力的作用,则重力与离心力的合力方向只能垂直于波面。当各个水质点做逆时针轨圆运动时,则到下一时刻,P1将从波峰处下来,P2会向波峰位置运动,P3将向P2所处的相位运动……这样,波浪就从左向右传播推进。这种表面波形可以用数学中的坦谷曲线表示,所以称为坦谷波。
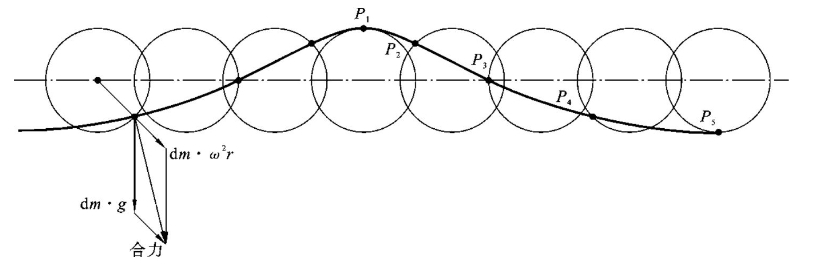
图8-21 水质点做轨圆运动时的受力
坦谷曲线的数学表达形式可以这样确定:设半径为R的圆盘在x轴上向右滚动,在圆盘上距离圆盘圆心为r的P点随圆盘滚动而产生的轨迹就是坦谷曲线,如图8-22所示。设圆盘滚动过程中的转速为ω,时间t后圆心到达O'位置,P点到达P'位置,则圆盘滚动的距离OO'=ωR·t,此时P'点在x轴上对应的坐标值为ωR·t+r·sinωt,P'点在y轴上对应的坐标值为-(R+r·cosωt),得到描述坦谷曲线的方程式为
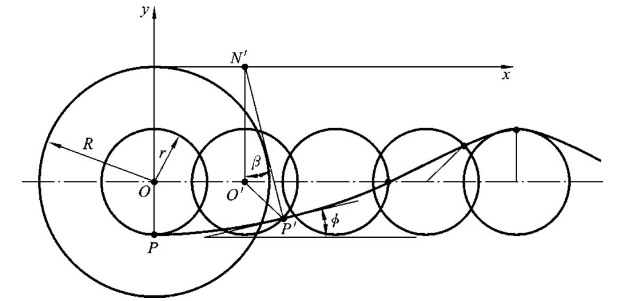
图8-22 表面波形的表达

根据图中所示的几何关系,P'点处坦谷曲线的斜率为
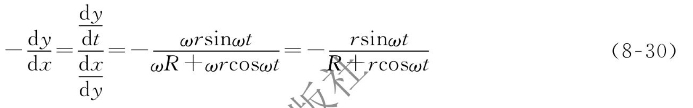
设过P'点的坦谷曲线切线与水平线的夹角为φ,则有

作过O'点的垂线与x轴相交于N'点,连接N'点与P'点,根据P'点的坐标,依几何关系有
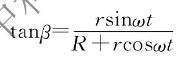
所以,
![]()
即
![]()
由于O'N'垂直于水平线,但β=φ,则N'P'必定垂直于P'点处的波面。进一步结合P'点处水质点做轨圆运动时重力、离心力的作用力大小与方向的关系(见图8-21),可得关系式:
 (https://www.xing528.com)
(https://www.xing528.com)
即

这就是波面水质点做轨圆运动的角速度的表达式。
在波浪传播过程中,波面上的水质点仅做轨圆运动,并不随波浪的传播向远处持续移动。波面上水质点轨圆运动经历一个周期,则波浪传播也经历一个周期,并且波浪向前推进一个波长。已知波面上水质点轨圆运动的角速度ω,则轨圆运动的周期为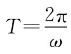 。
。
根据图8-22知,水质点P经历一个周期回到初始相位时,圆盘要滚动一个周长。圆盘的滚动相当于波浪的传播,设波浪的传播速度为C,则圆盘滚动的速度也为C,那么圆盘滚动一个周长的时间为![]() ,所以
,所以
![]()
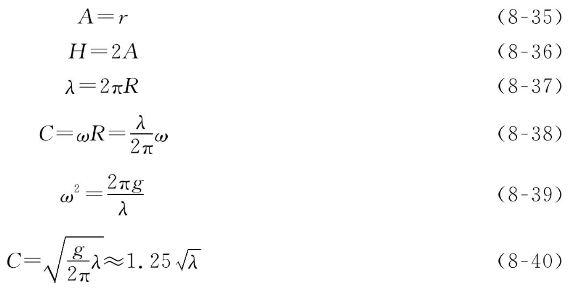
圆盘滚动一个周长相当于波浪经历一个波长λ,波幅A是指波面水质点轨圆运动的半径r,波高H是波面水质点最高点与最低点的高度差,则对于规则波,有
以上讨论的是波面处水质点的运动和波浪的传播。在波面以下的水质点同样也做同周期的轨圆运动,不过水质点轨圆运动的半径随水深的增加呈指数级衰减,且有
![]()
式中 z——波面上的水质点到水面的距离,m;
A——波幅,m。
下面对表达波浪的各要素及各要素之间的关系做统一说明。
波长λ与波速C的关系式为

波长λ与波浪周期T的关系式为

波长λ与波浪圆频率ω的关系式为

波速C与周期T的关系式为

波速C与波浪圆频率ω的关系式为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




