快速确定舰艇黏压阻力的方法

对于舰艇的黏压阻力，由于船体形状复杂，形状特征难以简单描述，并且黏压阻力受艉部流动分离的情况影响很大，而对流动分离进行准确计算也十分困难，所以目前还不能像对摩擦阻力那样总结出公认的计算公式，但是好在对一般的舰艇而言，黏压阻力所占比重都不大。

休斯为了提出更好的用于预报舰艇黏性阻力（包括摩擦阻力和黏压阻力）的方法，曾开展过确定舰艇黏压阻力方法的研究。在研究过程中，休斯开展了一系列的平板和平底船阻力测量试验，试验中雷诺数最高达到3×108。基于对试验结果的数据分析处理，休斯提出了船舶总阻力系数的计算公式：

式中　Cf——二维无曲率且展长无限大平板的摩擦阻力系数。

休斯建立的Cf计算公式为

该公式的计算结果与ITTC-57摩擦阻力系数计算公式接近，二者的差别是ITTC-57摩擦阻力系数计算公式包含船体表面的三维效应对摩擦阻力的影响，而休斯的摩擦阻力系数计算公式明确为二维无曲率且展长无限大平板的摩擦阻力系数计算公式。图8-18所示为休斯公式与ITTC-57公式在不同雷诺数下的对比。

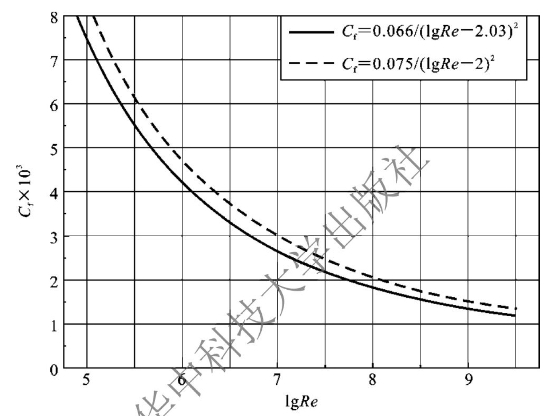
图8-18　休斯公式与ITTC-57公式在不同雷诺数下的对比

可见，在全雷诺数范围内，由休斯公式计算得到的摩擦阻力系数都比由ITTC-57公式所得的计算结果要略小。

黏压阻力系数Cpv实质上就是反映实际三维船体表面的黏性阻力（包括摩擦阻力与黏压阻力）与同等特征长度、同等面积、同等速度的二维光滑平板黏性阻力（此时只包含摩擦阻力）的差值，这个差值是因为船体三维外形而产生的，主要是黏压阻力，其实还包含船体的曲率对摩擦阻力影响，但黏压阻力占绝大部分。

需要指出的是，黏压阻力是因压差而形成的，摩擦阻力是因切应力而形成的，休斯提出的公式中是采用“形状阻力”这一表述，这样表述应该更准确，因为形状阻力是指由外形特征导致的压差阻力和摩擦阻力的变化量之和。本书中为了表达的统一，沿用黏压阻力的称呼。

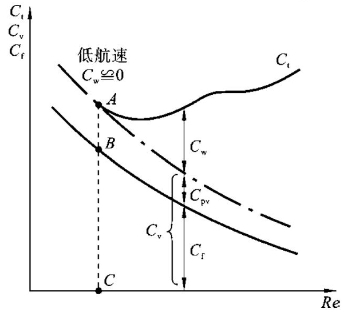
图8-19　船模阻力试验数据的处理

图8-19所示为休斯对船模阻力试验数据的处理。休斯认为，舰艇的兴波阻力占总阻力的比重随着航速的提高而迅速增加，当船模的速度很低时，如果船模的兴波阻力小到可被忽略，则此时总阻力系数Ct就等于摩擦阻力系数加上黏压阻力系数，如图8-19中，A点对应的总阻力系数的大小用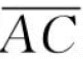表示，摩擦阻力系数用表示。对于一定的船模，速度越低雷诺数越小，根据摩擦阻力系数计算公式，摩擦阻力系数随着雷诺数的减小而增大，若速度低到兴波阻力可以忽略的程度，则就表示黏压阻力系数的大小，因此有(www.xing528.com)

令

则

式中　k——黏压阻力系数与摩擦阻力系数的比值；

1+k——形状因子。

形状因子被认为不随速度而变化，并且实船与缩尺船模的形状因子是相等的。所以，如果能确定舰艇的形状因子1+k，通过摩擦阻力系数计算公式获得舰艇在某一航速下的摩擦阻力系数后，就可以很方便地计算出黏压阻力系数Cpv和黏性阻力系数Cv了。

可见，确定黏压阻力系数的关键是先要确定形状因子，如果假定形状因子1+k不随航速的变化而改变，也不随船模尺度大小的变化而改变，而随着速度的降低舰艇的兴波阻力持续减小，那么可以认为

形状因子1+k的确定还可以通过普鲁哈斯卡法进行：针对缩尺船模开展船模阻力试验，并计算各速度下船模的摩擦阻力系数，然后将试验结果拟合，绘制成Cf随Fr（Fr=0.1～0.2）线性变化的直线，该直线的截距就是该船模的形状因子1+k，也是对应实船的形状因子。

需要注意的是，这种形状因子的确定方法对于方艉舰艇和船体上有非顺流向安装附体情况下的实船阻力预报可能会存在误差。因为对于方艉舰艇，当速度不高时方艉后部存在流动分离和旋涡，船体上非顺流向安装附体后部也存在旋涡，这类旋涡造成的黏压阻力是与舰艇的尺度有关系的，所以当用缩尺船模的形状因子替代实船的形状因子时会有误差。

另外，用普鲁哈斯卡法确定形状因子的前提是假定形状因子与船模的速度无关，这个假设在高航速时也许难以成立。因为在高航速下弗劳德数较大，舰艇或船模的航态将发生变化，船体吃水和船体纵倾角与低速时有很大不同，并且从雷诺数的角度来看，高航速与低航速时的雷诺数差别很大，船体绕流流态也不同，也会影响1+k的值。