舰艇船体阻力计算方法

弗劳德最早提出了将船体的摩擦阻力用同速度、同长度、同湿表面积的相当平板摩擦阻力来代替并计算。为了得出摩擦阻力的计算方法，弗劳德在托基的船模拖曳水池中开展了一系列的平板摩擦阻力试验。试验用的平板长度范围从10～50 ft（1 ft=0.3048 m）不等，平板表面采用虫胶清漆、石蜡、锡纸等多种不同的材料，以反映船体表面涂层和粗糙度的影响。每块平板浸深为19 in（1 in=25.4 mm），厚度为3/16 in，边缘都经过了倒圆角处理。经过系列平板试验，弗劳德提出了摩擦阻力的计算公式：

式中　S——平板的总面积，m2；

f——平板的摩擦阻力系数；

v——平板速度，m/s。

这个公式曾经长期在国际上被广泛采用，但是此公式最早出现在普朗特提出边界层理论（1904年）之前，也出现在雷诺提出表征流体黏性影响的雷诺数概念（1883年）之前，所以此公式没有从平板层流边界层、湍流边界层的本质去分析平板的摩擦阻力。但是弗劳德在试验中考虑了平板表面不同的材料和粗糙度，实践也证明该公式可以看成是计及了粗糙度的影响的，所以被广泛采用。

普朗特提出边界层理论后，人们才认识到边界层内壁面处流体速度法向梯度大小决定了局部切应力的大小，将平板上各处局部切应力积分就得到整个光滑平板总的摩擦阻力，而边界层内流体的法向速度分布又是由边界层内流体的流态和当地雷诺数大小决定的。由8.1.2节内容可知，整个平板的摩擦阻力可以采用无因次的平板摩擦阻力系数来计算：

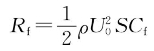
许多研究者开展了光滑平板摩擦阻力系数的研究工作，提出了一些受认可的光滑平板摩擦阻力系数的表达式。下面介绍几个有代表性的光滑平板摩擦阻力系数公式。

（1）勃拉齐层流边界层平板摩擦阻力系数公式，即

此公式适用于平板的边界层为层流边界层时平板摩擦阻力系数的计算。由于舰艇的尺度大、航速高，舰艇表面的边界层处于湍流边界层状态，所以该公式并不适用于舰艇摩擦阻力系数的计算。

（2）柏兰特-许立汀湍流边界层平板摩擦阻力系数公式，即

此公式适用于平板的边界层为湍流边界层时平板摩擦阻力系数的计算，在国际上有比较广泛的应用。

（3）桑海湍流边界层平板摩擦阻力系数公式，即

(www.xing528.com)

此公式是根据湍流边界层内速度沿平板法向按对数分布的假设，结合平板阻力试验结果而得到的，在1×106＜Re＜1×109的范围内，该公式可以转化为

（4）休斯湍流边界层平板摩擦阻力系数公式。

休斯认为在拟合平板摩擦阻力系数计算公式的测量试验中，使用的平板都是宽度有限的三维平板，三维效应会使得测量的摩擦阻力系数结果偏大。休斯将试验结果经过修正后得到了适用于计算无限宽度的二维湍流边界层平板摩擦阻力系数公式：

（5）1957年国际船模试验池实船-船模换算公式（ITTC-57公式）。

上述的湍流平板层摩擦阻力系数公式具有不同的形式，在计算船舶摩擦阻力时计算结果必然存在差异，1957年召开的国际船模试验池会议（International Towing Tank Conference，ITTC）专门针对船舶摩擦阻力的计算以及缩尺船模阻力到实船阻力换算的问题，提出了船模和实船相当平板摩擦阻力系数的计算公式：

此公式的作用主要是用于缩尺船模阻力到实船阻力换算，所以称为1957年国际船模试验池实船-船模换算公式，常简称为ITTC-57公式。

应用以上五种公式计算得到的不同雷诺数下的平板摩擦阻力系数的计算结果对比如图8-5所示。

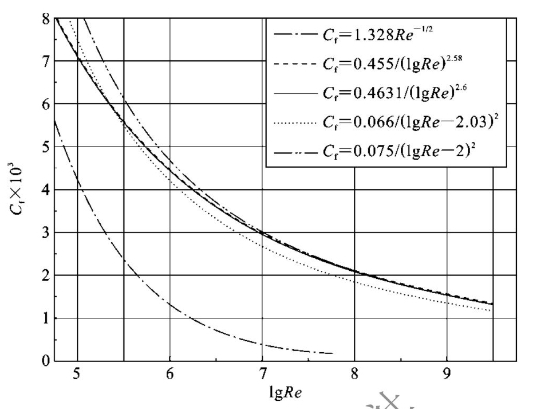
图8-5　各种平板摩擦阻力系数计算公式结果的对比

实际船体的浸湿表面并不是平板，船体表面存在纵向曲率和横向曲率（见图8-6），使得实际船体的边界层流动和摩擦阻力与同速度、同长度、同湿表面积的相当平板的摩擦阻力有一定的差异。

图8-6　舰艇水下船体表面

船体表面曲率的存在会导致当地船体摩擦阻力系数与同雷诺数的当地光滑平板摩擦阻力系数不一致，由于全船水下船体表面的横向、纵向曲率变化复杂，要准确计算整个船体曲率对摩擦阻力系数的影响十分困难，而研究表明曲率引起的摩擦阻力系数的变化并不大，所以一般并不针对曲率的影响单独进行计算，而是在船模向实船阻力换算中合并处理。