舰艇静力学快速逼近-舰艇静力学与快速性

逐步近似法往往用于大舱浸水时计算舰艇破损后的浮态和初稳性。所谓“大舱”是相对小舱而言的，在前面推导小舱的计算公式时，假定在吃水改变的范围内，船体和破损舱是直舷和直壁的，在倾角改变的范围内初稳性公式适用，在浮态改变的范围内破损舱类型不变等等。如果实际情况与以上假定的差别较大，就可能导致较大的计算误差。当某个破损舱采用小舱公式计算不能得到准确的结果时，可以认为这种舱为大舱。

以下介绍逐步近似法的要点。为方便起见，假设舰艇对称浸水，只引起纵倾，没有横倾。

1.第一次近似计算

第一次近似计算的方法和步骤与小舱浸水计算完全一样。

设舰艇原正浮于水线WL处，舰艇诸元为V、Sw、xf、h及H，如图6-5所示。有一对称大舱破损，破损舱诸元为v（xv，0，zv）、a（xa）、iax、iay。

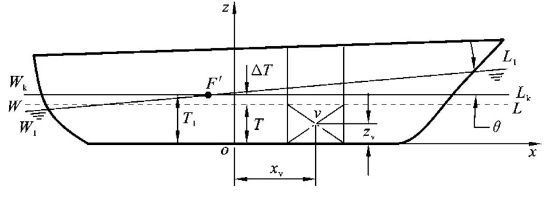
图6-5　大舱浸水第一次近似计算

根据小舱浸水计算公式可求舰艇浮态。

1）平均吃水的改变量

舰艇平均下沉至水线WkLk时平均吃水的改变量为

2）有效水线面形心的位置

有效水线面的形心F'的纵坐标为

3）损失惯性矩

损失惯性矩为

4）纵稳性高

破损后舰艇的纵稳性高为

5）纵倾角

纵倾角为

6）舯吃水

舯吃水为

通过上述计算，按照第三类小舱的计算公式（式（6-19）至式（6-32））不难得到第一次近似计算水线W1L1下要素V1（xb1，zb1）、Sw1（xf1）、Ix1、Iyf1，以及破损舱诸元v1（xv1，zv1）、a1（xa1）、ia1x、ia1y。

注意，上述各量中舰艇的水线元及破损舱的损失面积诸元均是它们在基平面上的投影。

2.第二次近似计算

由第一次近似计算的结果，得到近似计算水线W1L1，根据舰艇的重量与水线W1L1下的浮力之差修正平均吃水，得到修正水线Wk1Lk1，确定修正水线Wk1Lk1下因重力与浮力不在同一条铅垂线上而产生的力矩，做补加纵倾角Δθ的计算，由此得到第二次近似计算水线W2L2，如图6-6所示。

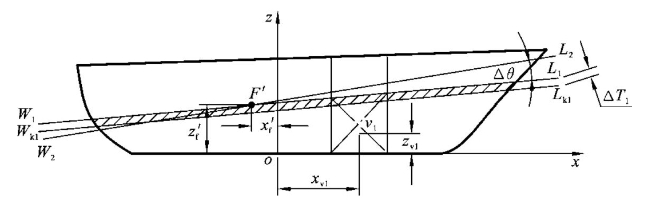
图6-6　大舱浸水第二次近似计算

1）平均吃水修正量(www.xing528.com)

按损失浮力法，水线W1L1下舰艇的浮力是ρg（V1-v1），则舰艇的重量P与浮力之差为

在直舷直壁假设下，平均吃水的修正量是：

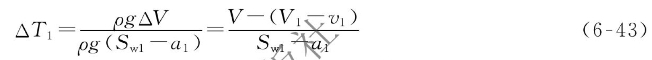
式中　ΔV——从水线W1L1下沉到水线Wk1 Lk1时舰艇的补加排水体积（如图6-6中阴影部分所示）。

经平均吃水修正，得到水线Wk1Lk1。

2）水线Wk1Lk1处的不平衡力矩及稳性高

首先要计算出水线Wk1Lk1处的有效诸元在基平面上的投影。

由于水线W1L1和水线Wk1Lk1很接近，故可以用水线W1L1处的有效水线诸元代替水线Wk1Lk1处的有效诸元，因此有效水线面在基平面上的投影面积为

有效水线面面积中心纵坐标在基平面上投影为

有效水线面面积在基平面上的投影的面积惯性矩为

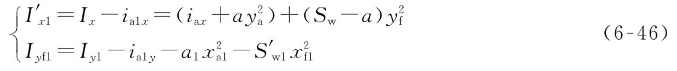
再计算出水线Wk1Lk1对应的舰艇诸元。

按损失浮力法考虑时，舰艇重量为P，重心为G（xg，0，zg），浮力则由几个部分的排水体积提供，即

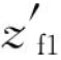排水体积V1的中心坐标为（xb1，zb1）、排水体积v1的中心坐标为（xv1，zv1）、排水体积ΔV的中心坐标为（），其中排水体积ΔV的中心可近似认为在水线W1L1处的有效面积中心（）上，而=T1+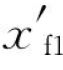tanθ1，于是水线Wk1Lk1之下有效排水体积中心坐标将是：

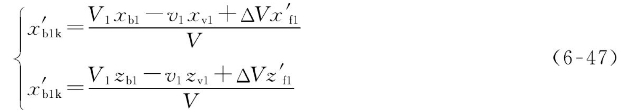
相当于舰艇沉至水线Wk1Lk1处时的初稳性高为

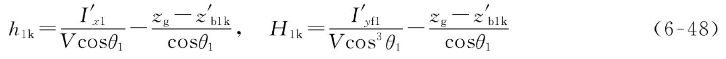
3）纵倾角的修正量Δθ1

舰艇在水线Wk1Lk1处时，由重力和浮力所形成的纵倾力矩及补加纵倾角Δθ计算式如下（见图6-7）。

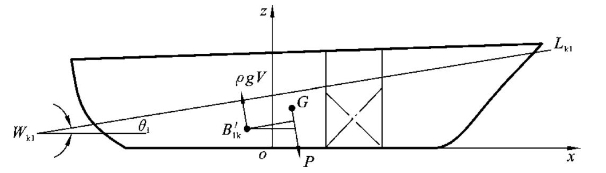
图6-7　大舱浸水第二次近似纵倾力矩计算

纵倾力矩：

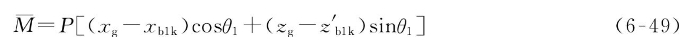
补加纵倾角Δθ1：

至此，得到在水线Wk1Lk1处的第二次近似值，其中舯吃水和纵倾角分别为

如果Δθ1比较小，计算至此可结束，否则应当再以由第二次近似计算得到的水线W2L2为原始水线，按上述步骤求第三次近似值，但在实际应用一般算到第二次近似值已够了。