舰艇动稳性曲线与应用

1.动稳性曲线

舰艇在静倾力矩和动倾力矩作用下产生倾斜的特点可概括如下：

舰艇在静倾力矩作用下，横倾角速度很小，可近似认为等于零。静倾力矩MKP作用于舰艇过程中始终与复原力矩Mr相平衡。因此，舰艇的静稳性是以复原力矩来衡量的。

舰艇在动倾力矩作用下横倾时具有角速度。只有当动倾力矩所做的功完全与复原力矩做的功抵消时，舰艇的角速度才变为零而停止倾斜。因此，复原力矩做功的大小标志着抵抗动倾力矩的能力，即动稳性。

当舰艇横倾至φ0时，复原力矩Mr所做的功为

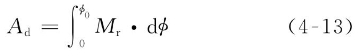
式中复原力矩Mr=P·lr随横倾角φ的变化规律由静稳性曲线（见图4-6（a））表示。式（4-13）也可以改写如下：

式（4-14）中Ad称为舰艇复原力矩抵抗倾斜时所做的功，反映了舰艇抵抗动倾力矩的能力，ld=·dφ称为动稳性力臂。Ad和ld随φ角而变化的规律用动稳性曲线（见图4-6（b））表示。

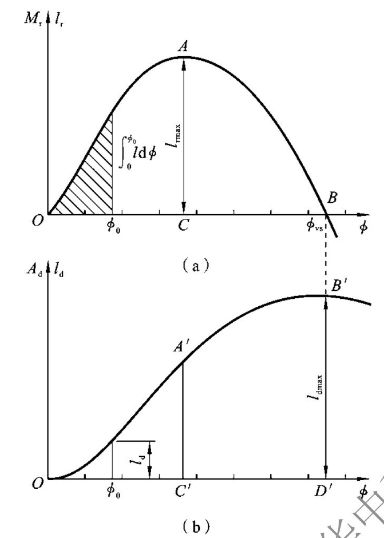
图4-6　静稳性曲线与动稳性曲线

根据定义知，动稳性曲线在几何上表现为静稳性曲线的积分曲线。有了静稳性曲线就可以用近似计算方法求出动稳性曲线。表4-2是根据静稳性曲线用梯形法计算动稳性曲线的一个实际例子。

表4-2　动稳性曲线的计算

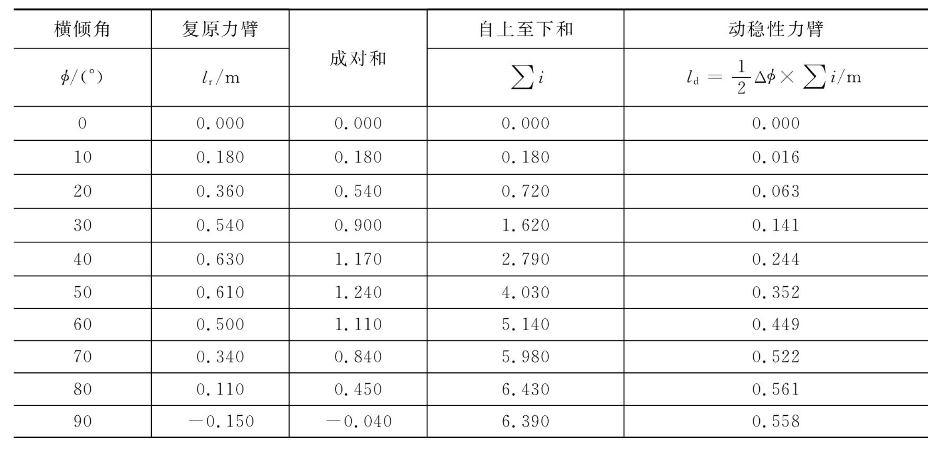
因为静、动稳性曲线是微分、积分关系，因此：

（1）在φ=0处，复原力臂lr=0，动稳性臂ld也等于零，这是ld的最小值。

（2）当φ等于最大静倾角φmax时，复原力臂达到最大值lrmax，在动稳性力臂ldφ曲线上对应点A'。

（3）当φ=φvs时（见图4-4），lr=0，动稳性力臂ld达到最大值ldmax。

（4）动稳性曲线在某一倾角处的纵坐标值代表静稳性曲线从原点至该处所围的面积，例如在图4-6中，动稳性曲线的纵坐标A'C'代表静稳性曲线图的面积SOAC；动稳性曲线的纵坐标B'D'代表静稳性曲线图的面积SOAB。

2.用动稳性曲线确定动倾角

假设有动倾力矩MKPD作用在处于正浮状态的舰艇之上。用静稳性曲线确定动倾角时，必须移动直线BG来使两个面积相等（见图4-5（a）），这样做比较麻烦同时也不够准确。用动稳性曲线来求动倾角φd时，把动倾力矩做功

画在动稳性曲线图中，就是斜率等于MKPD且过坐标原点的直线。因此在图4-7中，从横坐标轴原点量取57.3°（1 rad）到E点，再沿纵轴量取MKPD得到直线EK，连接OK直线，则该直线就是动倾力矩做功曲线，而复原力矩做功

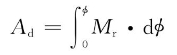(www.xing528.com)

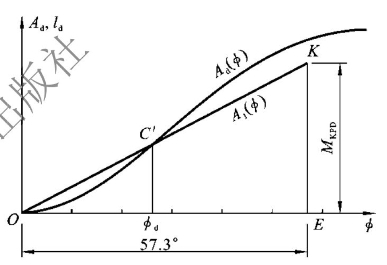
图4-7　在动稳性曲线上确定动倾角

表现在动稳性曲线图上就是动稳性曲线。在直线A1（φ）与曲线Ad（φ）的交点处动倾力矩与复原力矩做功相等，于是交点对应的角度就是动倾角φd。

3.正浮状态下舰艇的倾覆力矩Mc0（力臂lc0）

当舰艇在正浮状态下受到动倾力矩的作用时，舰艇能够抵抗的最大动倾力矩MKPDmax也就是使舰艇倾覆的最小力矩，称为正浮状态下舰艇最小倾覆力矩，记为Mc0，对应的力臂称为正浮状态下舰艇最小倾覆力臂，记为lc0。

正如前面已指出的，在静稳性曲线上（见图4-8（a）），使面积SOFG=SGHK的力矩即为最大动倾力矩Mc0，相应的动倾角φdc0即为正浮时的极限动倾角。

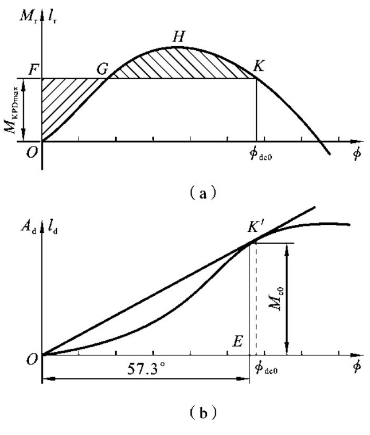
图4-8　正浮状态下舰艇倾覆力矩

在动稳性曲线图上，过O点作与动稳性曲线相切的切线OK'（见图4-8（b）），该切线表示以直线斜率为动倾力矩的做功曲线。若增加直线OK'的斜率，则动倾力矩做功大于复原力矩做功，所以，直线OK'的斜率就是舰艇在正浮状态下的最小倾覆力矩Mc0（力臂lc0）。从坐标原点量取φ=57.3°，从坐标原点量取切线上对应点的纵坐标值，该值便是切线的斜率，即舰艇在正浮状态下的最小倾覆力矩Mc0（力臂lc0）。而切点K'相对应的动倾角便是正浮时极限动倾角φdc0。

4.有初始横倾角时舰艇的倾覆力矩Mc（力臂lc）

动倾力矩（如突风吹袭）并不总是在舰艇正浮状态时发生，普遍的情况是舰艇在航行中因风浪的作用产生摇摆运动，摇摆至某一横倾角φ1时又受到动倾力矩的作用。有两种极端的情况：一种是舰艇横摇至右舷（倾角为φ1）并要向左舷摇摆时，受到来自左舷的突风作用阻摇；另一种是舰艇横摇至左舷（倾角为φ1）并要向右舷摇摆时，受到来自左舷的突风作用助摇。不难分析后一种情况下舰艇所能承受的动倾力矩较前一种情况下要小许多，即后一种情况是最危险状况。因此，《舰船通用规范》中要求针对后一种状况进行大角稳性的校核，规定有初始横倾角时舰艇所能抵抗的最大动倾力矩为倾覆力矩Mc（力臂lc）。

在静稳性曲线上确定倾覆力矩的方法与正浮时类似。如图4-9所示，在静、动稳性曲线图上，反向延长曲线（注意静稳性曲线是关于坐标原点对称的，而动稳性曲线是关于纵坐标轴对称的），使图4-9（a）中面积SAFH=SHKL，即两阴影部分面积相等，则对应的动倾力矩即为有初始横倾角的倾覆力矩Mc（力臂lc），L点对应的横倾角是有初始横倾角时的极限动倾角φdc。

同样，在动稳性曲线上（见图4-9（b）），从A'点作动稳性曲线的切线，切点为L'。从φ1开始在横坐标轴上量取57.3°到E'点，过E'点作垂线，分别与直线A'L'和过A'点的水平线交于点D'、B'，D'B'便对应倾覆力矩Mc（力臂lc）。切点L'对应的横倾角则为极限动倾角φdc。

由前述可知，从静、动稳性曲线上都可以确定倾覆力矩Mc（力臂lc），当然所得到的结果也是一致的。在静稳性曲线上要作出两个面积相等的曲边三角形不容易保证精度，所以一般在动稳性曲线上量出倾覆力矩Mc（力臂lc）。

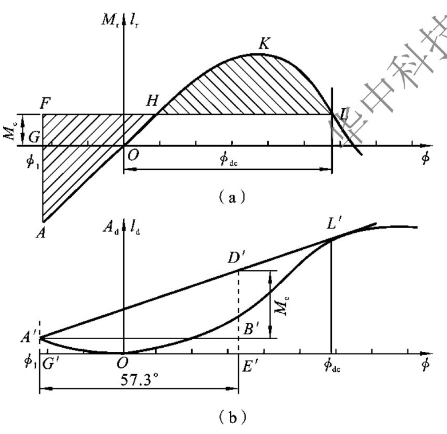
图4-9　有初始横倾角条件下的舰艇倾覆力矩

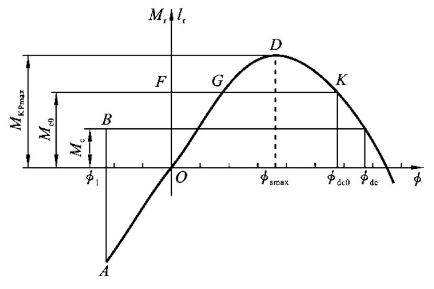
图4-10　舰艇倾覆力矩和极限横倾角

本节介绍了三个极限力矩——舰艇所能承受的最大静倾力矩MKPmax，正浮状态下舰艇的倾覆力矩Mc0和有初始横倾角时舰艇的倾覆力矩Mc，以及三个对应的极限角度——φsmax、φdc0和φdc。这三个极限力矩（极限角度）反映了不同状态下舰艇抵抗外力的能力。由于MKPmax＞Mc0＞Mc（见图4-10），可以认为Mc反映了舰艇在波浪中航行时抵抗外力的最大能力，所以，在《舰船通用规范》中以Mc作为校核舰艇大角稳性的依据。而在对舰艇进行横向补给时，因受到承载索的牵引力作用，初始横倾角比较小，便以Mc0作为校核舰艇横向补给时的大角稳性的依据。MKPmax反映的是舰艇抵抗静倾力矩的稳性能力，在舰艇的建造、维修和改装中往往需要以MKPmax作为实际工作中保证抵抗静力矩作用能力的依据。此外，极限角度是从横倾角度来反映舰艇抵抗外力的稳性能力的，因角度比力矩更具直观性，某些船级社也有采用极限角度来校核船舶的稳性的。

几点说明：

（1）外力矩一般是随横倾角φ变化的，特别是风作用的倾斜力矩，而且多半是随着横倾角φ的增加而减小，美国的相关规范中假定风作用的倾斜力矩随cos2φ变化。在我国《舰船通用规范》中则取为常数，这样选取是偏于安全的。

（2）在解动稳性问题时，用动稳性曲线求解要比用静稳性曲线方便，省去了凑面积的步骤。但是动稳性曲线的这一优点，只有当外力矩的积分曲线是一条直线时才会显示出来（即外力矩为定值）。国外一些规范规定外力矩是变化的，在进行大角稳性计算时用静稳性曲线，所以用动稳性曲线计算并不一定是必须的。

（3）静力学中用功能平衡方法确定舰艇倾覆力矩Mc，与实际情况相比较是偏于安全的，即使舰艇倾覆的力矩要比Mc大。它没有考虑横倾的阻尼及附加质量的影响，因为阻尼及附加质量会使倾角减小。若再计及舰艇在波浪中的各种动力影响，情况将更加复杂。舰艇在波浪中的稳性是需要研究的一个课题。