静力学与快速性：探究静稳性曲线意义

舰艇发生大角度倾斜时，仍然是用舰艇倾斜后产生的复原力矩来表示阻止舰艇倾覆的能力，此时复原力矩随横倾角的变化规律已不能像初稳性研究中用简单的公式（见式（3-10））表达，而需要以曲线形式给出。这里将假定舰艇处于静水之中，水线面为一水平面，并且忽略舰艇在横倾时由于船体艏、艉不对称所引起的纵倾的影响，即不考虑它们之间的耦合作用。

如图4-1（a）所示，设舰艇原正浮于水线WL处，重量为P，重心在G点，浮心在B点，等体积倾斜一大角φ到达水线WφLφ。这时，舰艇的重心保持不变，由于排水体积形状发生变化，浮心位置由B点沿某一曲线移动到Bφ点。于是重力P和浮力ρgV形成一个复原力矩，且有

式中　Mr——复原力矩；

lr——复原力臂。

与小角度倾斜时的初稳性所不同的是：首先大角度倾斜时等体积倾斜轴线不再通过正浮水线面的漂心。因为小角度倾斜时，出、入水楔形体剖面（见图3-2）可近似为直角三角形，从而导出出水端与入水端水线面对倾斜轴的面积静矩相等，但随着倾角增大，将楔形体剖面近似为直角三角形带来的误差将增加。其次是相应的浮心移动曲线也不再是圆弧的一段。初稳性计算中把浮心移动曲线近似为圆弧，随着倾角增大，浮心移动曲线与圆弧的偏差也会增大。所以式（4-1）不再能表达成像初稳性公式那样的简单解析形式。

在大角稳性计算中，一般将复原力矩与横倾角的关系以曲线图的形式呈现出来，如图4-1（b）所示。该曲线图表示了舰艇在不同倾角时复原力矩的大小，称为静稳性曲线。初始阶段复原力矩随横倾角的增大而单调增加，这是由于初始阶段出、入水楔形体体积和体积中心移动距离随横倾角增加而增加，当上甲板入水以后，出、入水楔形体体积的增加和移动距离逐渐减缓，达到某一横倾角时复原力矩达到最大值。其后，随着横倾角的进一步增大，出、入水楔形体体积和体积移动距离开始减小，相应的复原力矩也随之减小，直至复原力矩降低到零，进而变为负值。静稳性曲线表示舰艇在某一载重状态下复原力矩与横倾角的关系。由于式（4-1）中复原力矩Mr与复原力臂lr之间仅相差一个倍数即重量P，可以在静稳性曲线图上用同一条曲线表示它们，只是纵坐标要采用不同比例尺。

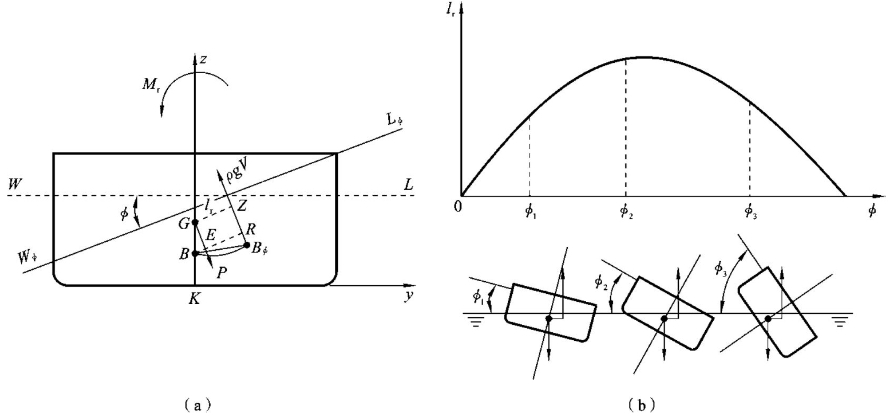
图4-1　舰艇大倾角倾斜受力分析

与第3章分析复原力矩物理意义式（见式（3-16））相类似，将大角度倾斜时的复原力矩也分成船形稳性力矩与重量稳性力矩（见图4-1）：

式中　Mf——船形稳性力矩，Mf=P·；

Mw——重量稳性力矩，Mw=-P·。

船形稳性力矩是由水密体积的移动造成的。如图4-2所示，出水、入水楔形体体积均为v，则船形稳性力矩为

船形稳性力矩总是沿着使舰艇恢复到原平衡位置的方向。(www.xing528.com)

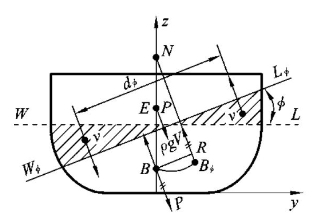
图4-2　船形稳性力矩与重量稳性力矩

重量稳性力矩为

它的大小取决于重心在浮心以上的高度。一般水面舰艇重心总在浮心之上，所以重量稳性力矩的作用效果总是使舰艇偏离平衡位置。

若以复原力臂表示舰艇大角稳性，则有

式中　lf——船形稳性力臂，lf=；

lw——重量稳性力臂，lw==asinφ，其中a=zg-zb是重心距浮心的高度。

基于在一般情况下船形及重量分布的左右对称性，静稳性曲线是关于坐标原点的对称曲线，故而通常只画一半。

静稳性曲线的基本用处包括：

（1）确定舰艇在各种外力作用下的倾角；

（2）衡量舰艇在一定载重状态下稳性的好坏；

（3）作为计算舰艇抗风浪性的基本资料。