舰艇载荷水平纵向移动的表现

载荷水平纵向移动所产生的纵倾角的计算方法，与水平横向移动时类似。载荷q自A1点水平纵向移动至A2点，移动的距离为xq2-xq1，如图3-17所示。船的重心自G点水平移动至G1点，舰艇将产生纵倾，并浮于新的水线W1L1处，其纵倾角为θ，根据重心移动定理可得：

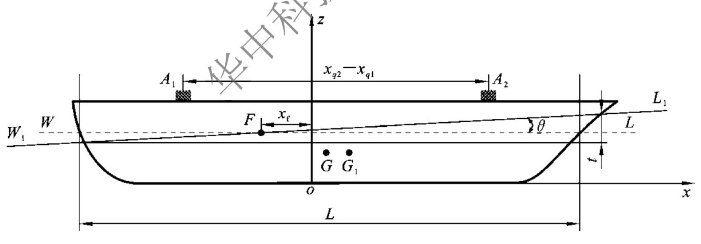
图3-17　载荷的水平纵向移动

3.2.1小节已经证明，等体积倾斜水线面W1L1与原水线面WL的交线必然通过原水线面的形心F。这样艏、艉吃水的变化可以从图3-17中的几何关系求得：

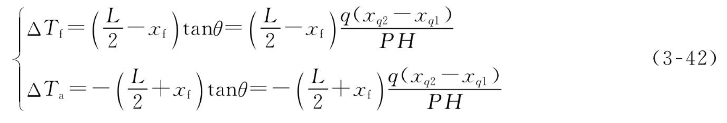
新的艏、艉吃水为

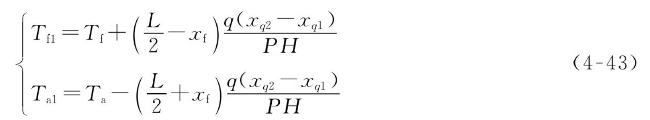
与载荷水平横向移动类似，载荷水平纵向移动时，舰艇将产生纵倾，而初稳性基本不变。

由于舰艇的纵向尺寸较大，纵倾角较小，故一般舰艇的纵倾常采用艏艉吃水差t来表示。舰艇艏艉吃水差为

为了比较方便快速地确定外力矩引起的舰艇艏艉吃水差，常用到每厘米纵倾力矩。定义舰艇产生1 cm艏艉吃水差所需的外力矩为每厘米纵倾力矩，记为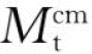（有的资料用符号MTC表示）。每厘米纵倾力矩在数值上就等于舰艇艏艉吃水差为1cm时的纵倾复原力矩。为此，令t=Tf-Ta=1 cm，因为吃水差与纵倾角之间关系为

所以当艏艉吃水差为1 cm时，舰艇相应的纵倾角为

吃水差为1 cm时相应的舰艇复原力矩为

由式（3-45）计算所得的力矩值就是使舰艇产生1 cm吃水差所需的外力矩大小，因此，舰艇每厘米纵倾力矩为

由于浮心和重心之间的距离zg-zb与纵稳心半径R相比是一个小值，可以认为H≈R，因此式（3-46）也可写成：

若已知外加的纵倾力矩Mt，则由每厘米纵倾力矩可以求得艏艉吃水差：

注意：每厘米纵倾力矩和每度横倾力矩都是随排水量和重心高度而改变的。(www.xing528.com)

例3-3　某驱逐舰因装载不当形成艏纵倾，已知艏吃水Tf=3.80 m，艉吃水Ta=3.40 m，问：要将艏部燃油舱中多少燃油导移至艉舱才能使该舰恢复正浮？假设艏、艉燃油舱的容积中心相距l=90 m，船长L=110 m。

解　方法一：

吃水差

相应的艏纵倾

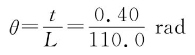
从正浮位置纵倾至该角度时舰艇的复原力矩应为PHθ，为求出P、H，可利用静水力曲线。根据平均吃水（3.80+3.40）/2 m=3.60 m查该舰艇的静水力曲线得：

欲使舰艇恢复正浮，必须使导移燃油所形成的力矩和上述复原力矩相等，于是可得：

则

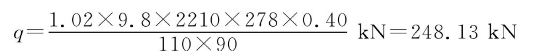
方法二：

先求出每厘米纵倾力矩，再按平均吃水3.60 m，从静水力曲线上查出V、Iyf的值，并算出纵稳心半径R。再根据H≈R，求出H值。

每厘米纵倾力矩为

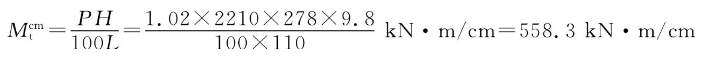
现有纵倾差为

欲消除40 cm纵倾差，所需力矩大小为

需导移燃油的重量为

可见，由以上两种解法所得的结果是一样的，且若已知每厘米纵倾力矩（有的静水力曲线包括每厘米纵倾力矩随吃水改变的曲线），则计算更为简便。