舰艇静力学与快速性：移动的浮心

如果使舰艇在横剖面内做不同倾角（如10°，20°，30°，…）的等体积倾斜，由于水下体积形状不断改变，浮心位置也将不断地改变。若这种等体积倾斜进行了一周，即转动了360°，那么浮心的移动轨迹将是一条封闭的空间曲线。由于舰艇艏、艉的不对称性，当做横向的等体积倾斜时，浮心不仅会在横剖面上移动，还将产生纵向的移动。

从理论上讲，研究舰艇横倾时浮心移动的变化规律，应当以浮心空间移动轨迹为对象，但为了简化问题，一般以浮心移动轨迹在横剖面上的投影，即浮心曲线，取代其实际轨迹。这相当于忽略了浮心在纵向的移动，而浮心的纵向移动将引起舰艇的纵倾，所以也就是忽略了由横倾引起的纵倾。考虑到浮心纵向移动所引起的纵倾通常都很小，所以这样做不会带来显著的误差。

考察图3-4，浮心曲线有如下特性：

图3-4　浮心移动曲线

（1）浮心曲线在某点的切线平行于相应水线。这是因为当舰艇自水线WL向某一方向倾斜（如右倾）一小角度时，根据重心移动定理，浮心自点B移动到点B1，直线段BB1与g1g2平行（g1、g2分别是出水、入水楔形体的体积中心），所以浮心不仅向倾斜方向移动，并且兼有高度方向（z轴方向）上的移动，于是对WL水线而言，点B与浮心曲线上左右邻近点相比当然是处于最低点位置，那么过点B作平行于水线WL的平行线，所得到的必然是浮心曲线在点B处的切线。

（2）浮心曲线在某点之法线垂直于相应水线，并且和相应的浮力作用线在横剖面上的投影相重合。这一点是很明显的：既然切线平行于水线，那么法线必然垂直于水线，而浮力作用线在横剖面上的投影也必然通过该点并垂直于水线，二者完全重合。

以下分析舰艇倾斜后浮心移动距离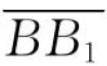的大小。如图3-4所示，设舰艇漂浮于水面并处于平衡状态时的水线为WL，排水体积为V，横倾一小角度φ后倾斜水线为W1 L1。令v1、v2分别表示出水及入水楔形体的体积，g1、g2分别表示出水、入水楔形体的体积中心。由于v1=v2，因此可以认为：舰艇在横倾至水线为W1L1时的排水体积不变，只是出水楔形体部分排水体积移到了入水楔形体处，相应的排水体积中心从g1移至g2。利用浮心移动定理，可以求得浮心移动距离为

且。由于v1=v2，所以，代入式（3-2）得：

(www.xing528.com)

式（3-3）右端是出水楔形体积对倾斜轴线O—O的静矩。从图3-2、图3-3中可以看出：

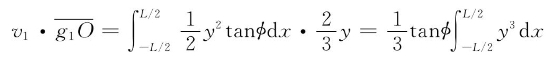
当φ为小角度时，tanφ≈φ，故

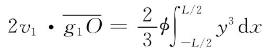
积分式为水线WL对应水线面的面积对纵向中心轴线O—O的面积惯性矩Ix，因此：

将式（3-4）代入式（3-3）中，得

由式（3-5）可见，浮心移动的距离与面积惯性矩Ix、横倾角φ成正比，而与排水体积V成反比。