舰艇平衡方程式化简-舰艇静力学与快速性

将舰艇的平衡条件用数学方程式的形式表达就是平衡方程式。

以下针对舰艇的四种漂浮状态写出平衡方程式。

1.正浮状态下的平衡方程式

如图2-7所示，由于船体左右对称，舰艇正浮时，浮心必在中线面上，根据平衡条件，重心坐标yg也必然在中线面上，故有

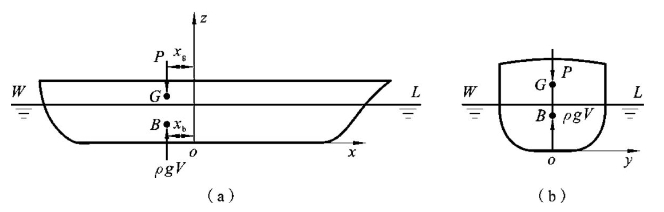
图2-7　舰艇在正浮状态下的受力

2.横倾状态下的平衡方程式

如图2-8所示，可导出舰艇在横倾状态下的平衡方程式为

3.纵倾状态下的平衡方程式

同理，不难由图2-9导出舰艇在纵倾状态下的平衡方程式：(www.xing528.com)

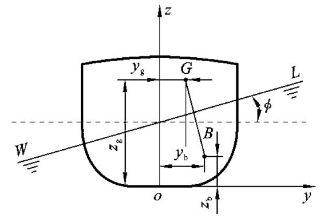
图2-8　舰艇横倾状态

图2-9　舰艇纵倾状态

4.任意状态下的平衡方程式

任意状态下的平衡方程式可以直接由式（2-5）和式（2-6）得出：

一般横倾状态和任意状态下的平衡方程式在实际中较少使用。利用平衡方程式，可以检查某已知水线（即吃水、横倾角、纵倾角均为已知）是否为平衡水线（即该已知的漂浮状态是否为平衡状态）。为此，需求出舰艇的重量、重心坐标、水下体积（浮力）和浮心坐标，把这些值代入以上平衡方程式中看其是否成立即可判定。

由舰艇的平衡条件或平衡方程式可知，舰艇重量、重心坐标、浮力和浮心坐标共同决定了舰艇的漂浮状态，在后续章节讨论的稳性问题也是重量和浮力的相互作用问题。因此，舰艇静力学研究始终围绕着这几个量展开，讨论其变化规律和计算方法。