车辆稳控技术匹配原理整车匹配提高效率

稳控系统匹配时需要确定上百种工况下的临界滑移率对应的轮加减速度和参考滑移率特征，使用传统的方法需要耗费大量的金钱和时间。根据耗散功率方法能自适应各种路面附着状况的特点，考虑将耗散功率原理应用于稳控系统与整车的标定匹配中。根据耗散功率原理可知，耗散功率极值对应的滑移率略小于临界滑移率且相差不大，在各种路面条件下，附着系数利用率均可达到90%以上。因此可以采用耗散功率极值对应的滑移率代替峰值附着系数对应的滑移率对稳控系统进行控制。而滑移率与耗散功率曲线获得较为简单，一种工况对应的曲线原则上只需要一次制动实验即可，比之传统的需要上百次实验确定一组曲线的匹配方法，大大提高了匹配效率。为了使耗散功率原理更符合实际情况，对载荷转移、滑移率、耗散功率进行分析，以某高附着路面为例，其滑移率与纵向附着系数曲线如图6-5所示，峰值附着系数为0.78，临界滑移率为0.17。首先在仿真平台上使用单轮模型，在上述高附路面上进行常规制动，获得的滑移率、耗散功率曲线如图6-6所示，其耗散功率极值为9.2463×10⁴N·m/s，对应的滑移率为0.14。在仿真平台上使用双轮模型（7自由度模型），为了对比方便，前后轮的轮胎结构参数（质量、刚度、转动惯量等）完全一致，仍然在同样的高附路面上进行常规制动，获得的前后轮的滑移率-耗散功率曲线如图6-7所示，其中前轮的耗散功率极值为1.2246×10⁵N·m/s，对应滑移率为0.13；后轮的耗散功率极值为6.1333×10⁴N·m/s，对应的滑移率为0.14。

图6-5 滑移率与纵向附着系数曲线

图6-6 单轮模型的滑移率与耗散功率关系

(www.xing528.com)

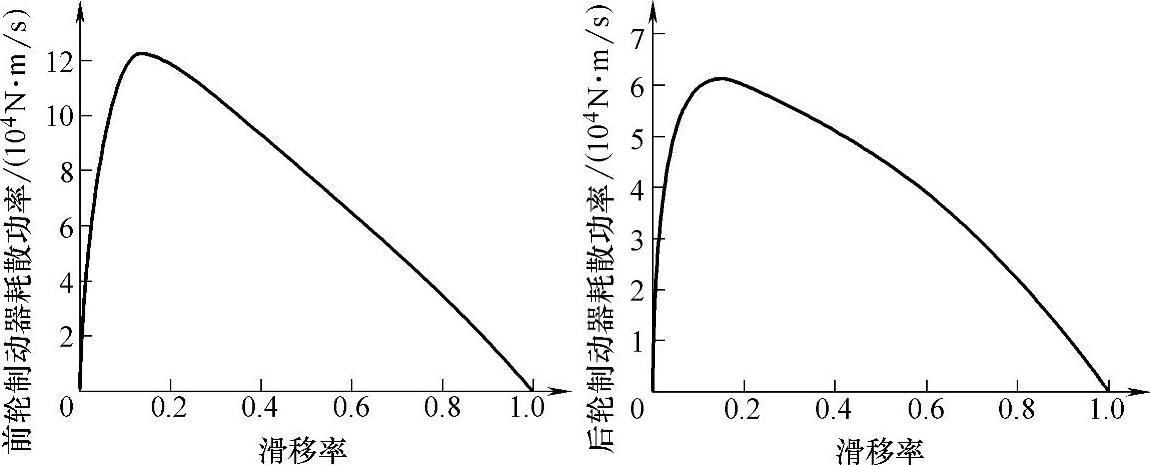
图6-7 双轮模型的滑移率与耗散功率关系

根据分析可以得到如下结论：

1）无论双轮模型还是单轮模型，其耗散功率极值对应的滑移率均接近临界滑移率，且耗散功率极值对应的附着系数与峰值附着系数接近，附着系数利用率均达到98%以上。

2）单轮模型和双轮模型的计算结果有所区别，说明载荷转移会对耗散功率的计算带来影响。在考虑载荷转移后，耗散功率的极值不同；但其极值对应滑移率差别小，极值对应的附着系数差别也很小。

由于匹配时只关心峰值附着系数处的特征，而耗散功率极值对应的附着系数与峰值附着系数接近，可以用极值对应的附着系数处的特征对稳控系统进行匹配。