车辆稳定控制技术-压力估计算法

根据稳控系统控制要求，每个控制周期都需要进行制动轮缸压力估计。当前周期的制动轮缸压力可以由上周期的制动轮缸压力和本周期的轮缸压力腐化率得到。由于制动轮缸压力估计的初始条件为轮缸压力为零，所以每个周期的制动轮缸压力可以看做是制动轮缸压力变化率对时间的积分，因此对制动轮缸压力的估计相当于对每个周期的轮缸压力变化率的估计。制动轮缸压力估计流程如图3-18所示。

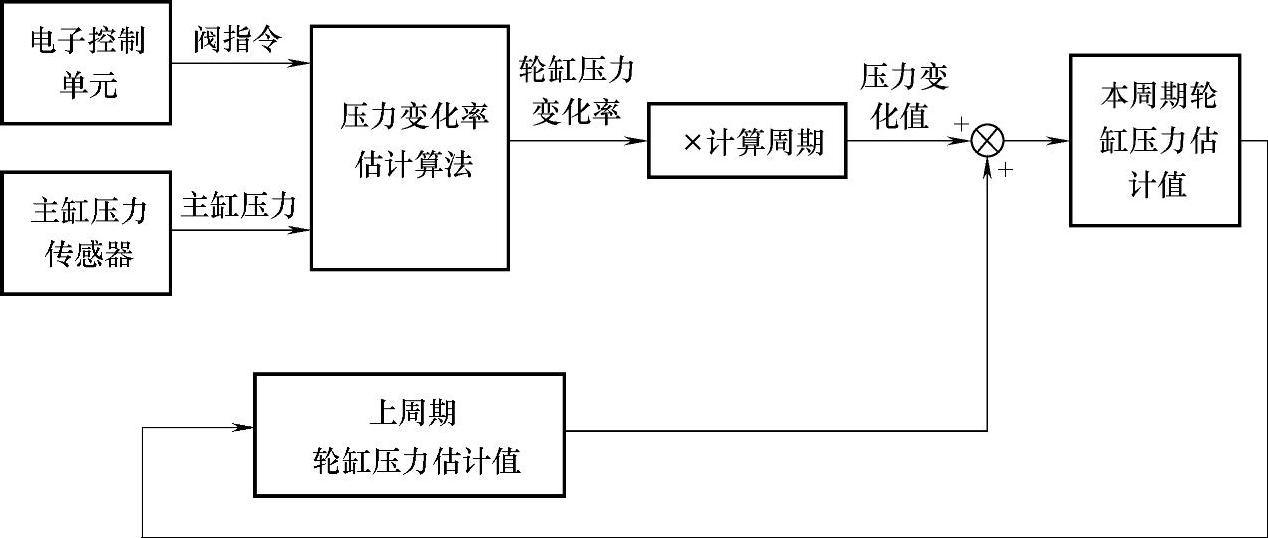
图3-18 制动轮缸压力估计流程框图

基于上节研究，制动轮缸压力变化率根据电磁阀的状态可以分为三个部分：

1）增压速率，由主缸压力及主缸与制动轮缸间的压力差确定。

2）减压速率，由制动轮缸压力确定。

3）压力变化率的补偿，即对于电磁阀状态切换和增减压的初始阶段的补偿，以及对电磁阀状态切换带来的压力滞后的补偿。

由于制动系统复杂，增减压速率与主缸压力、压力差和制动轮缸压力的关系难以用准确的数学模型来描述；即使得到数学模型，由于计算量太大也无法应用于资源有限的单片机中。模糊推理可以不依赖对象的数学模型，是处理非线性问题的有力工具，并且模糊推理可以在单片机中实现。当电磁阀状态为常态时，轮缸压力变化由主缸压力及主缸与轮缸间的压力差决定。构造如图3-19所示的模糊推理模型，以主缸压力和压力差为输入，增压速率为输出。该模型为多输入单输出的模糊推理模型。

模糊模型的建立包括论域的设定、隶性度函数的选择与划分、模糊规则的确定和输入的模糊化及输出的反模糊化等。将实车实验测量得到的主缸压力、压力差和增压速率的数据对作为给定的专家经验，按照经验和对制动系统的定性研究解释模糊模型，从而确定合适的隶性度函数和模糊规则。由于模糊推理本身不具备自学习功能，其对基于数据建模的应用受到了限制。人工神经网络具有自学习功能，但不能表达模糊语言，类似一个黑箱，不能很好地利用经验知识，从而增加了训练时间或者陷入局部极值。若能够将模糊推理和神经网络二者有机地结合起来，则既能够发挥二者的优点，又可以弥补各自的不足。将神经网络的自学习方法应用于对模型特性的分析和建模上，产生自适应神经网络技术，将自适应神经网络技术用于模糊推理系统的隶属函数和模糊规则的确定，形成自适应神经模糊推理系统。自适应神经网络模糊推理方法可以基于大量已知数据建立模糊规则。自适应神经网络模糊推理方法如图3-20所示。

图3-19 增压速率模糊推理模型

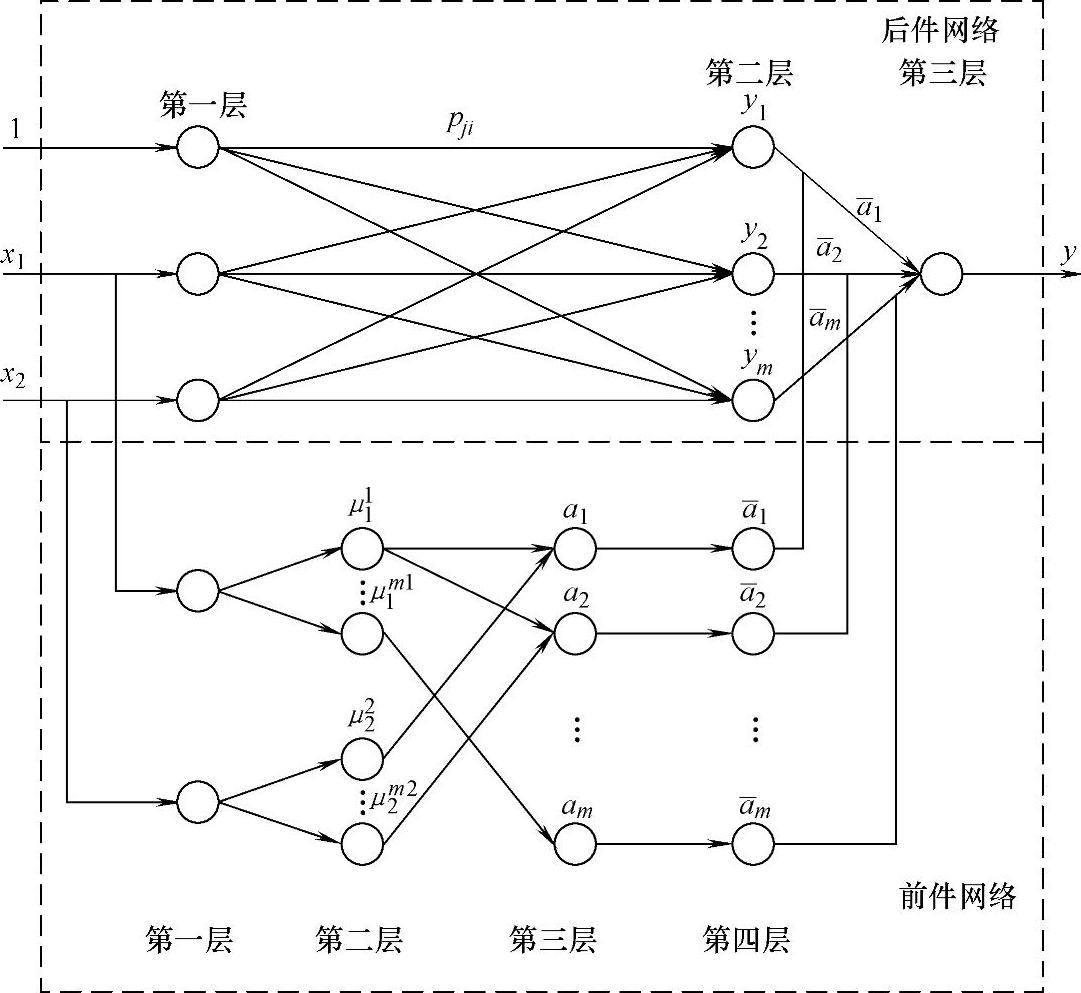
图3-20 自适应神经网络模糊推理图

（1）建立模糊推理系统

建立模糊神经网络系统（图3-20）的输入为主缸压力、主缸与制动轮缸间的压力差，其模糊输入语言变量分别用x₁、x₂表示；系统的输出为增压速率，用y表示。本网络由前件网络和后件网络组成，前者用来匹配前件模糊规则，后者用来产生后件模糊规则。

（2）确定模糊推理隶属度函数与模糊规则

通过实车实验获得大量的主缸压力、压力差与增压速率的数据对，将数据对输入上述模糊神经网络系统中进行学习训练。训练得到的模糊推理系统示意图如图3-21所示。

图3-21 训练得到的增压速率模糊推理系统示意图

对得到的增压速率模糊推理系统进行验证，以一组实车测试的增压曲线（左前轮缸数据）为例，其主缸压力、压力差如图3-22所示。

图3-22 实车测试得到的主缸压力、左前轮缸压力及压力差

不考虑增压初期的压力波动，仅考察增压阶段，将主缸压力和压力差输入模糊推理系统，输出为增压速率的估计值，估计值与实测值如图3-23所示，满足稳控系统使用需要。与增压速率的估计方法类似，构建减压速率的模糊推理系统如图3-24所示。

图3-23 增压速率的估计值和实测值

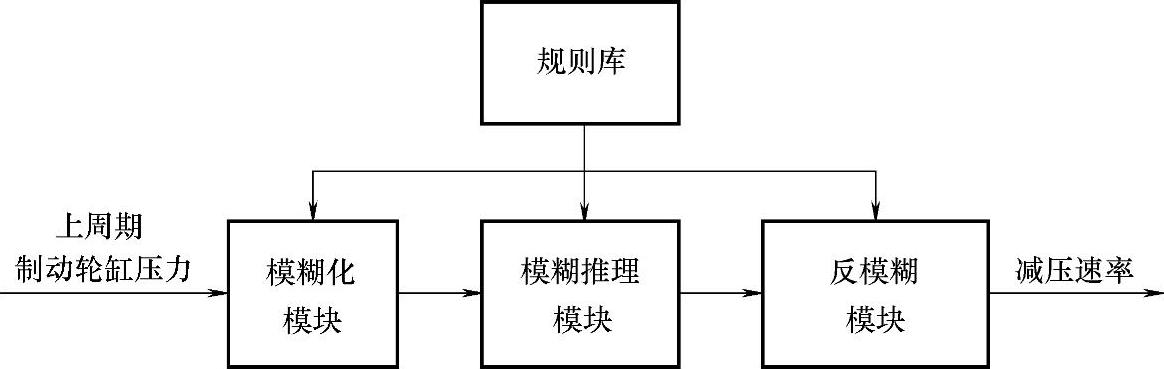
图3-24 减压速率模糊推理系统

构建的模糊推理系统为单输入单输出系统，输入为当前的制动轮缸压力，输出为减压速率。将大量实车实验数据输入系统进行学习训练，得到减压速率估计的模糊推理系统，训练方法与增压速率的训练方法相似。以一组实车测试的减压曲线为例，其轮缸压力如图3-25所示。

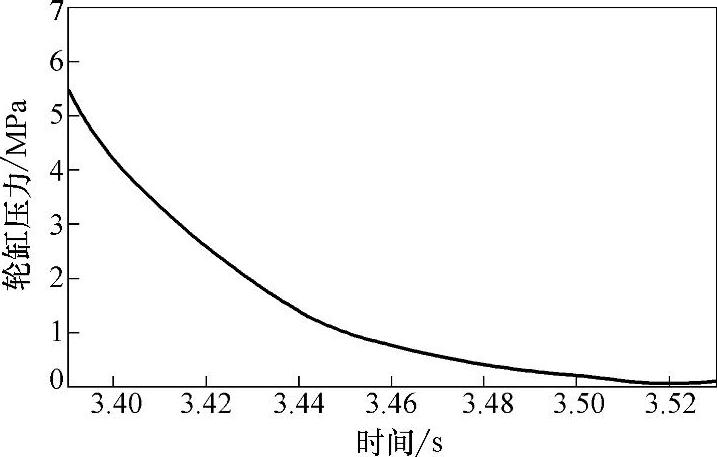
图3-25 减压时轮缸压力的实车实验数据

将轮缸压力输入减压速率估计模糊推理系统，输出即为减压速率。图3-26所示为估计得到的减压速率和实测的减压速率对比。在电磁阀进行状态切换时，压力的响应有滞后，并且切换到增压和减压的初期压力有波动，其增减压速率无法通过正常的压力速率模糊推理过程得到，因此需要进行补偿。

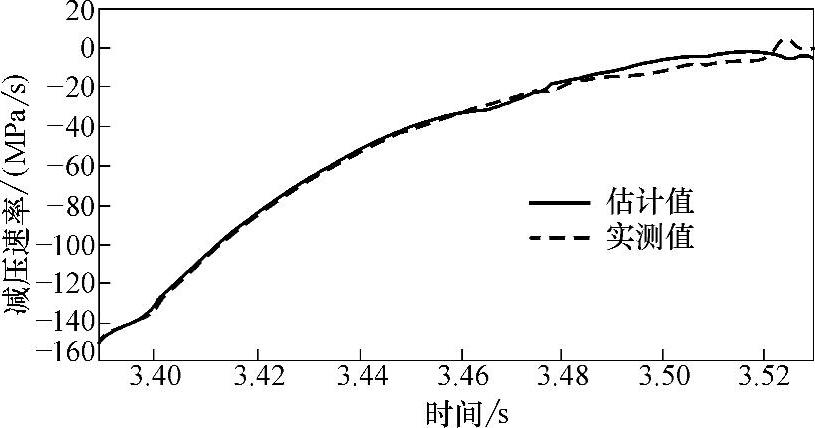
图3-26 减压速率估计值与实测值

（1）对于切换到增压和减压的初期阶段压力波动的补偿。

当电磁阀状态由保压或减压状态切换到增压状态时，在较短的一段时间内压力会有波动，如图3-27所示。当电磁阀状态由增压或保压状态切换到减压状态时，会出现初始减压阶段压力波动。

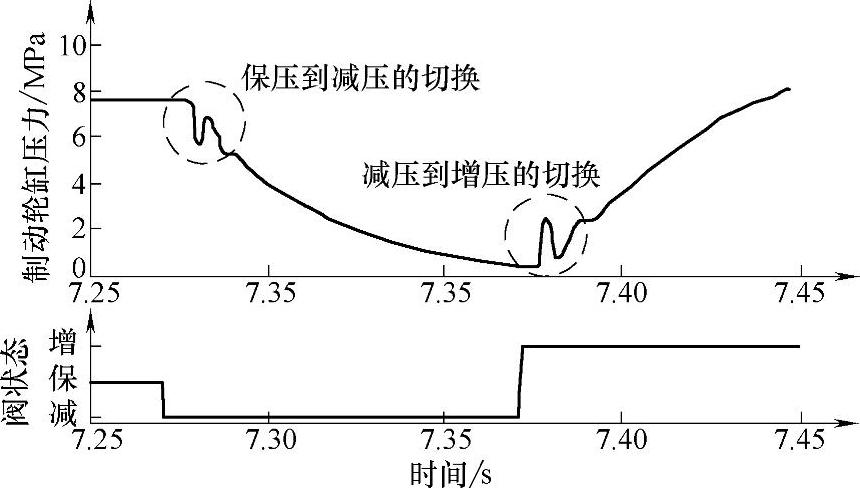
图3-27 初始增压和减压阶段的压力波动

由实车数据分析可知，初期的压力波动速率和后续的压力变化率差别较大，如果采用模糊推理的方法对波动速率进行估计，则会大大增加模糊规则的设计难度和计算量，因此本章采用对初始压力波动进行补偿的方法。对实车的两段增压过程进行研究：第一段增压属于普通增压阶段，历时32ms，由5.287MPa上升到8.119MPa，其轮缸压力、主缸压力和增压速率如图3-28所示，用曲线“1”标识；第二段增压包含初始增压阶段，轮缸压力由保压切换到增压，出现初始增压的波动，初始值5.287MPa，经历33ms，压力上升至8.07MPa，其轮缸压力、主缸压力和增压速率用曲线“2”标识。

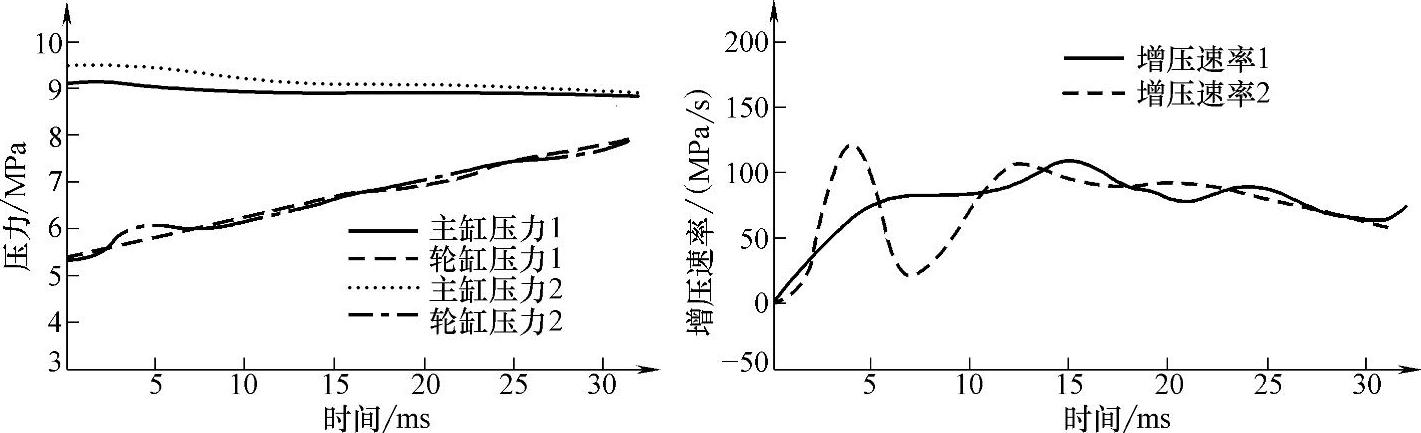
图3-28 普通增压过程和含初始增压阶段增压过程的实车数据对比

根据数据分析可知，两种增压情况的初始条件基本一致；两种增压情况增压速率相差较大，但在初始增压波动结束后，二者的增压速率趋于相同，且二者的轮缸压力接近一致。这说明在相同的初始条件下，当时间超过初始压力波动时间后，普通增压和初始增压经历相同的时间，其增压结果是相同的，如上例中，普通增压历时32ms，增压了2.832MPa，初始增压历时33ms，增压了2.792MPa。由于初始增压阶段的压力波动时间很短，一般在10ms以内，压力波动对于制动力矩的影响可以忽略，并且稳控系统的计算周期一般为10ms，相当于忽略了很短时间内的压力波动，但其增压的结果并没有变化。因此本章用普通增压阶段的增压速率估计来代替增压的初始阶段的增压速率，忽略了切换初期的压力波动。对于初始增压阶段的增压速率补偿进行验证，将图3-29所示的主缸压力和轮缸压力的初始条件输入普通增压速率模糊推理系统，得到增压速率估计值，以及按照增压速率估计得到的轮缸压力估计值与实测值对比，如图3-30所示。当压力由增压和减压切换到保压时，压力也有波动，在进行切换延迟的补偿后，忽略保压时候的压力波动，以稳定后的压力作为保压状态的压力。

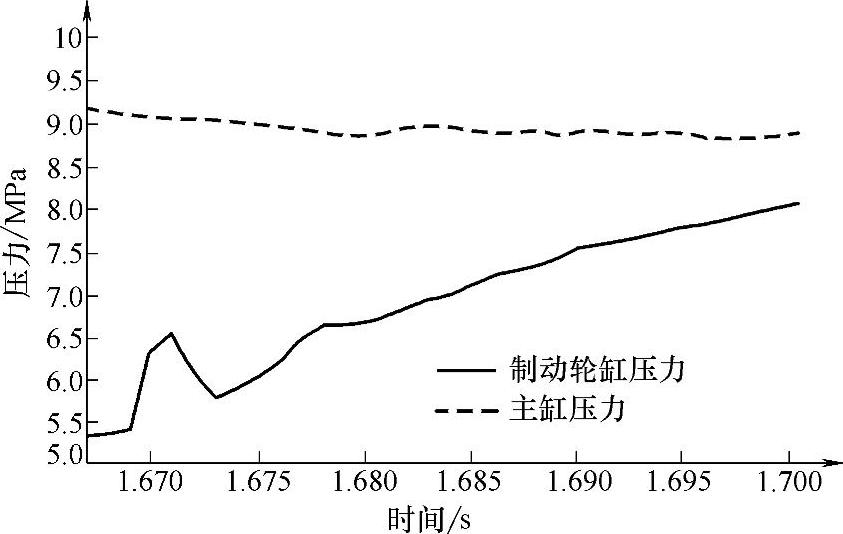
图3-29 实测的含有初始增压阶段的主缸和轮缸压力(www.xing528.com)

图3-30 模糊推理得到的估计值与实测值的对比

（2）对于电磁阀状态切换的压力滞后的补偿

在电磁阀状态切换时，压力响应有滞后。例如电磁阀处于减压状态，在t₀时刻电磁阀切换到增压状态，即t₀时刻发出增压命令，压力需要到t₁时刻才开始由减压变为增压，把t_d=t₁-t₀称为电磁阀由减压状态切换到增压状态的压力响应滞后时间。这个滞后时间已经包括电磁阀的开关响应、阀芯运动时间、制动轮缸因素等。由于制动轮缸压力是由电磁阀的状态经历时间和压力变化速率计算得到的，因此必须考虑电磁阀状态切换带来的压力响应滞后。例如在稳控系统控制过程的缓增压中，电磁阀状态在保压、增压之间反复切换，切换带来的滞后示意图如图3-31所示。

图3-31 缓增压状态切换示意图

对于缓增压中的一个阶段而言，由保压切换到增压的压力响应滞后时间为t_d0，本阶段电磁阀增压指令的时间为t_on（称之为期望增压时间），再由增压切换到保压的压力响应滞后时间为t_d1，因此实际处于压力上升状态的时间为t_p=t_on^-td0+td1，称t_p为实际增压时间。可见由于压力滞后的存在，实际增压时间与期望增压时间并不一致。同理，状态切换为减压或是保压时现象也类似。根据电磁阀切换的滞后特点研究得到以下补偿方案：电磁阀切换前状态为A，压力为p₀，在t0时刻切换为状态B，则t₁时刻（t₁＞t₀）的压力p_t1按式（3-1）进行计算：

式中 A，B——A，B∈{增压，保压，减压}；

t_d——状态A切换到状态B的压力响应延迟时间；

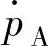——按照状态A估计的压力变化率；

——按照状态B估计的压力变化率；

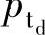——压力开始响应时的初始值，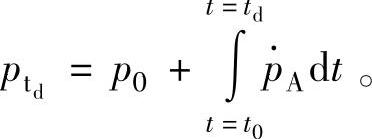

需要根据实车数据对状态切换的压力响应延迟时间t_d进行标定，包括保压切换到增压、减压切换到增压、增压切换到保压、减压切换到保压、增压切换到减压以及保压切换到减压六种状态的延迟时间。以由减压到增压的状态切换的补偿为例，其初始条件如图3-32a所示，将主缸压力、电磁阀状态，初始压力值2.6701MPa作为初始条件，根据阀状态和开启时间，用模糊逻辑推理估计增压和减压速率，并将压力变化率积分，得到轮缸估计压力值如图3-32b所示，阀状态切换的压力响应延迟没有补偿的估计值与实测值有一定误差；对阀状态切换压力响应延迟进行补偿的压力估计值与实测值基本吻合，从而证明了本补偿方法的必要性和有效性。制动压力的估计是从初始主缸压力和轮缸压力为零的状态开始的，因此制动轮缸压力可以通过制动轮缸压力变化率对时间积分得到，具体算法如图3-33所示。

图3-32 减压切换到增压的压力估计

图3-33 轮缸压力估计算法框图

对轮缸压力估计算法说明如下：

1）轮缸压力的估计算法中，主缸压力和阀的开关状态为已知量，主缸压力通过主缸压力传感器得到，阀的开关状态直接从电子控制单元的控制程序中得到。

2）压力估计的基本公式如式（3-2）所示。

式中 p（n）——第n个计算周期的分泵压力估计值；

p（n-1）——第n_-1个计算周期的轮缸压力估计值；

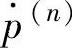——第n个计算周期的轮缸压力变化率的估计值；

t_c——计算周期。

3）每个计算周期根据电磁阀状态选择轮缸压力估计路径。

①如果处于电磁阀状态切换过程，则根据“状态切换补偿”估计压力变化率。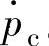

②如果处于非切换过程的增压状态，则根据“增压速率模糊推理”模块估计增压速率。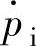

③如果处于非切换过程的减压状态，则根据“减压速率模糊推理”模块估计减压速率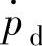

④如果处于非切换过程的保压状态，则保压压力不变。

4）增压速率估计的输入为主缸压力p^（n）_m（压力传感器测得）和主缸与轮缸间的压力差Δp^（n）（Δp^（n）=p_m^（n）-p^（n-1））。

5）减压速率估计的输入为轮缸压力p^（n-1）。

为了验证制动轮缸压力估计算法，进行如下实车实验：迅速踩下制动踏板并在整个实验过程中维持踏板位置；电磁阀状态由ECU预先设定的测试程序确定，其输出包括了稳控系统控制过程中电磁阀的各种状态，如直增压、缓增压、直减压、缓减压、保压、各种状态间的切换等，可以充分地验证压力估计算法。实车实验结果如图3-34所示。

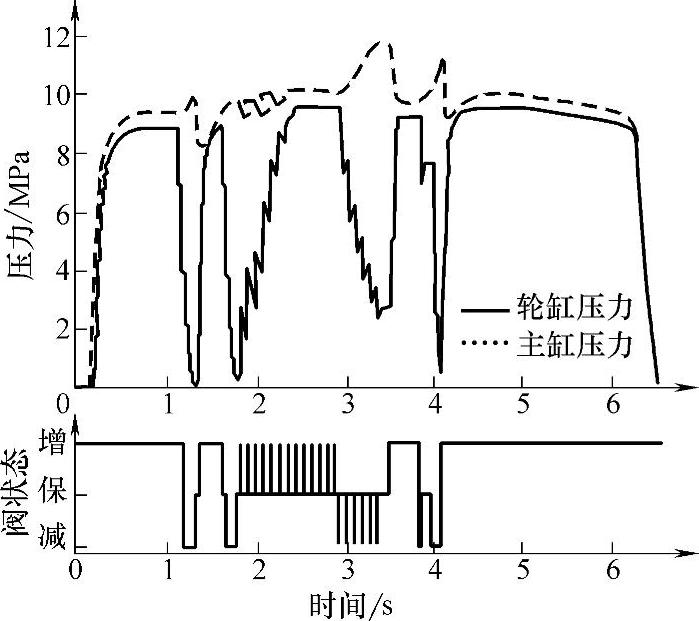
图3-34 制动系统压力综合变化实验结果

将上述实验中的主缸压力和电磁阀的时间经历状态作为轮缸压力估计的已知条件，其初始条件为主缸和轮缸压力均为零，轮缸压力估计值如图3-35所示。制动轮缸压力的估计值基本与实测值符合。为了对比更清楚，将实测压力与估计压力的1.7～2.2s的缓增压曲线放大显示在一张图上，如图3-36所示。轮缸压力估计值忽略了压力切换初期的压力波动，但总体压力水平与实测值保持一致，可以满足稳控系统控制的需要。根据制动轮缸压力变化特性，建立了轮缸压力变化率的模糊推理模型，并设计了压力变化率的补偿算法，提出了通过主缸压力估计制动轮缸的方法。该估计方法得到的轮缸压力与实测值符合程度很好，能够满足稳控系统需要。

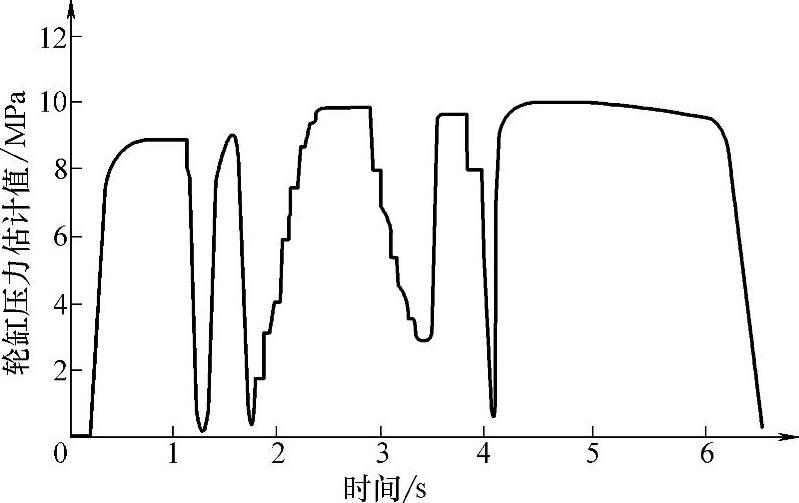
图3-35 制动轮缸压力估计结果

图3-36 缓增压过程的实测值与估计值对比